このページでは、数学Bの「漸化式」全10パターンをまとめました。
漸化式の見分け方と計算方法を、具体的に問題を解きながらわかりやすく解説していきます。
問題集を解く際の参考にしてください!

[toc]
1. 漸化式の公式
漸化式(ぜんかしき)と読みます。
数学B「数列」の分野で、重要な分野です。
漸化式の全10パターンをA4(PDF)にまとめました。

数字と \(n\) のある場所でどのタイプの漸化式なのか見分けます。
どのパターンかわかったら、初手を覚えてください。
例えば…
特性方程式型なら、特性方程式を使う。
分数型なら、逆数をとる。
指数型なら、両辺を \(q^{n+1}\) で割る。
対数型なら、両辺に \(\log\) をとる。
初手を覚えたら、あとは計算していくだけです。
このように、漸化式の問題では
① どのパターンか見分ける
② 初手を覚える
この2点が重要です。
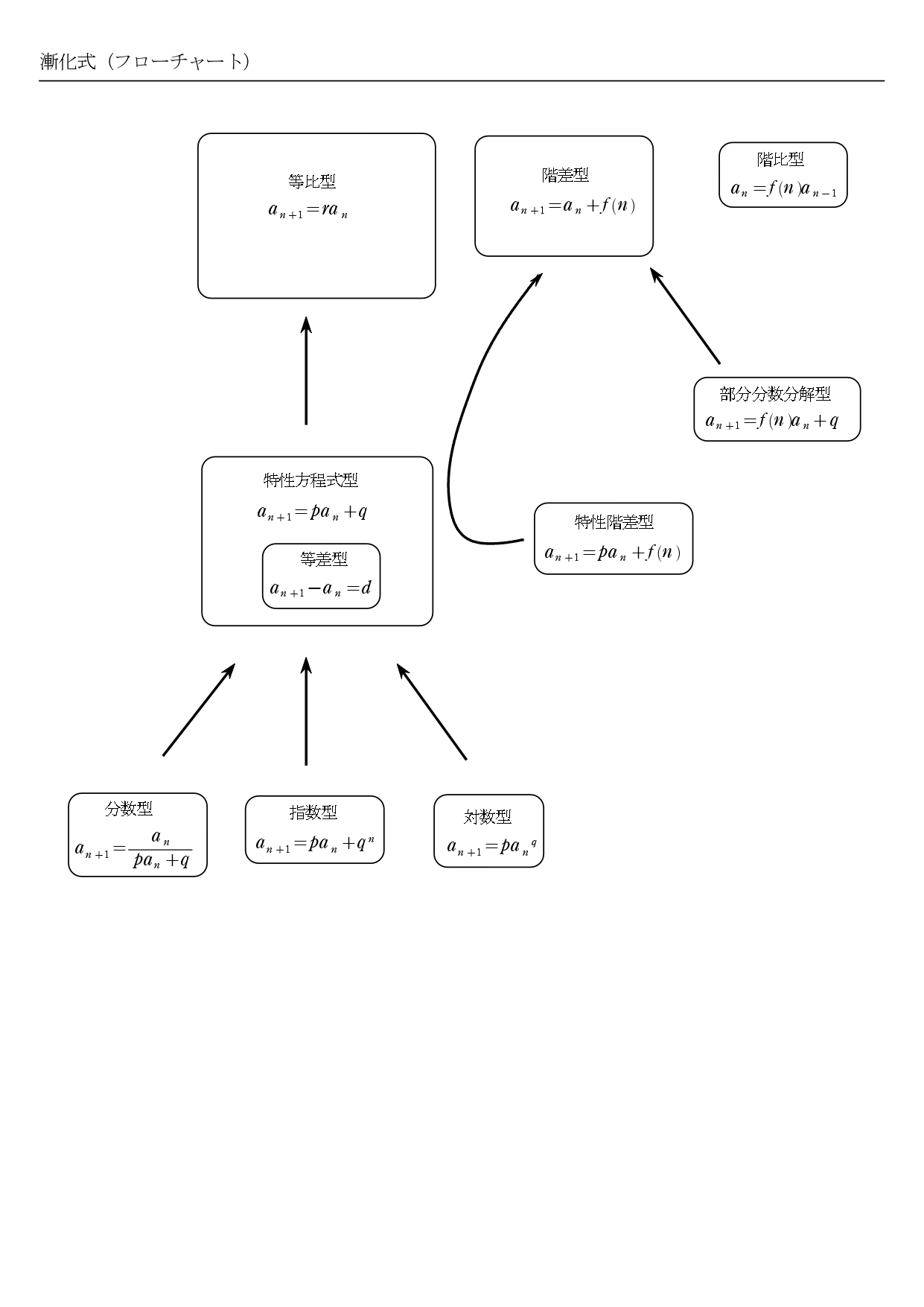
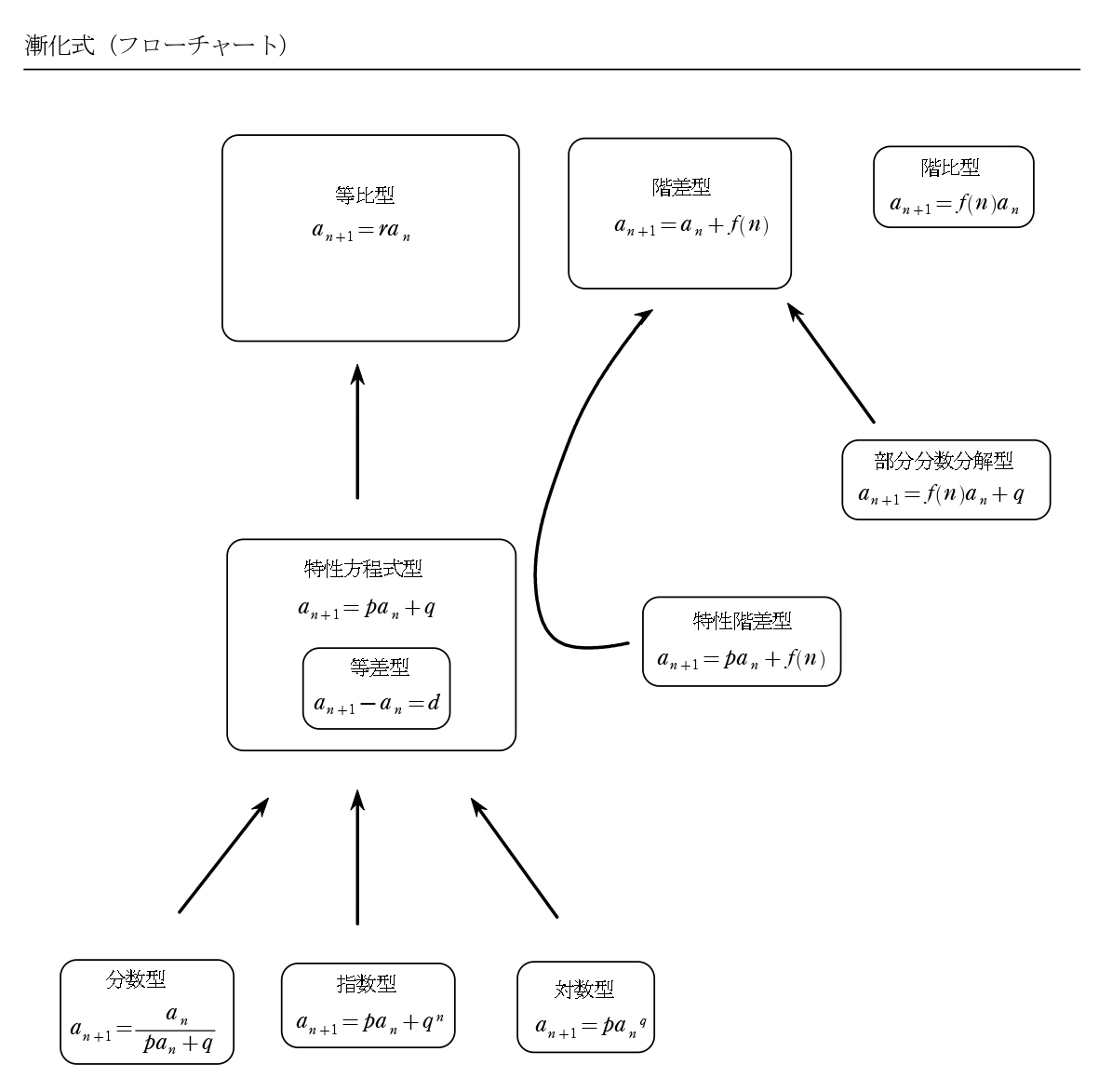
2. 漸化式のフローチャート
漸化式の公式をフローチャートでA4(PDF)でまとめました。
フローチャートを見れば、全10パターンの重要度がわかります。
やみくもに漸化式を解くのではなく、流れを理解してください。
等差型は、特性方程式型が \(p=1\) のときなので特性方程式型に包まれます。
分数型、指数型、対数型は、特性方程式型から等比型になります。
特性階差型のみ、特性方程式を経由して階差型になります。(等比型になりません)
また、部分分数型、階比型は例外なのがわかると思います。
次に、実際に問題をときながらわかりやすく解説していきます。
3. 漸化式の解き方
3.1 等差型
\(a_1=2\),\(a_{n+1}=a_n + 3 \) によって定められる数列\({a_n}\)の一般項を求めよ。

\(初項 \ 2 \ ,公差 \ 3 \ の等差数列なので\\ \\
a_n = 2+(n-1)・3 \\ \\
\hspace{ 10pt }= \color{#ef5350}{3n-1}\\
\)
3.2 等比型
\(a_1=1\),\(a_{n+1}=2a_n \) によって定められる数列\({a_n}\)の一般項を求めよ。

\(初項 \ 1 ,公差 \ 2 \ の等比数列\\ \\
a_n = 1・2^{n-1} \\ \\
\hspace{ 10pt }= \color{#ef5350}{2^{n-1}}\\
\)
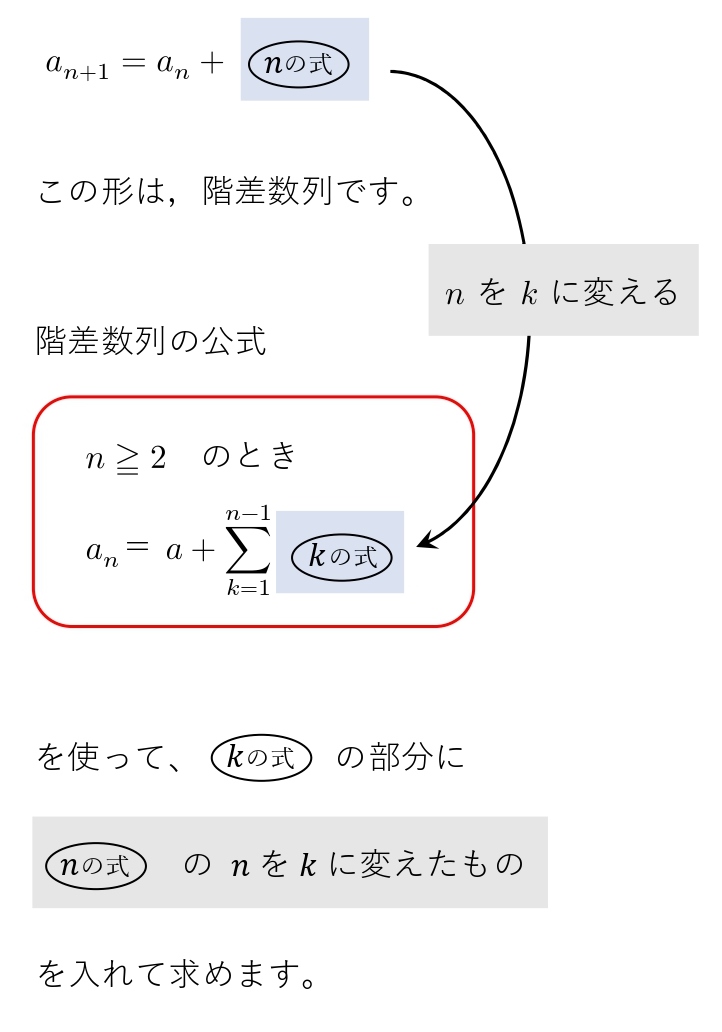
3.3 階差型
\(次の条件によって定まる数列 \ {a_n} \ の一般項を求めよ。\\ \\
(1) a_1=1,a_{n+1}=a_n+3^n \\ \\
(2) a_1=0,a_{n+1}=a_n+2n+1 \\
\)
\(
n ≧ 2 のとき\\ \\
a_n = 1+ \displaystyle \sum_{k=1}^{n-1} 3^k \\ \\
\hspace{ 7pt } = 1 + 3^1 + 3^2 + 3^3 + \cdots + 3^{n-1} \\ \\
\hspace{ 25pt } 初項 \ 1,公比 \ 3,項数 \ n \ の等比数列の和\\ \\
\hspace{ 10pt } = \displaystyle\frac{1・(3^n-1)}{3-1} \\ \\
\hspace{ 10pt } = \displaystyle \frac{3^n-1}{2}\\ \\ \\
n = 1 のとき\\ \\
a_1 = \displaystyle\frac{3-1}{2} \\ \\
\hspace{ 10pt } = 1 \\ \\ \\
よって\\ \\
a_n =\displaystyle \color{#ef5350}{\displaystyle{\frac{3^n-1}{2}}}\\
\)
\(
n ≧ 2 のとき \\ \\
a_n = 0+ \displaystyle \sum_{k=1}^{n-1} (2k+1) \\ \\
\hspace{ 8pt }= 2\displaystyle \sum_{k=1}^{n-1} k + \displaystyle \sum_{k=1}^{n-1} \\ \\
\hspace{ 8pt }= n(n-1) + (n-1) \\ \\
\hspace{ 8pt }= (n+1)(n-1) \\ \\ \\
n = 1 のとき \\ \\
a_1 = (1-1)(1+1) \\ \\
\hspace{ 8pt }= 0 \\ \\ \\
よって\\ \\
a_n = \color{#ef5350}{(n-1)(n+1)}\\
\)
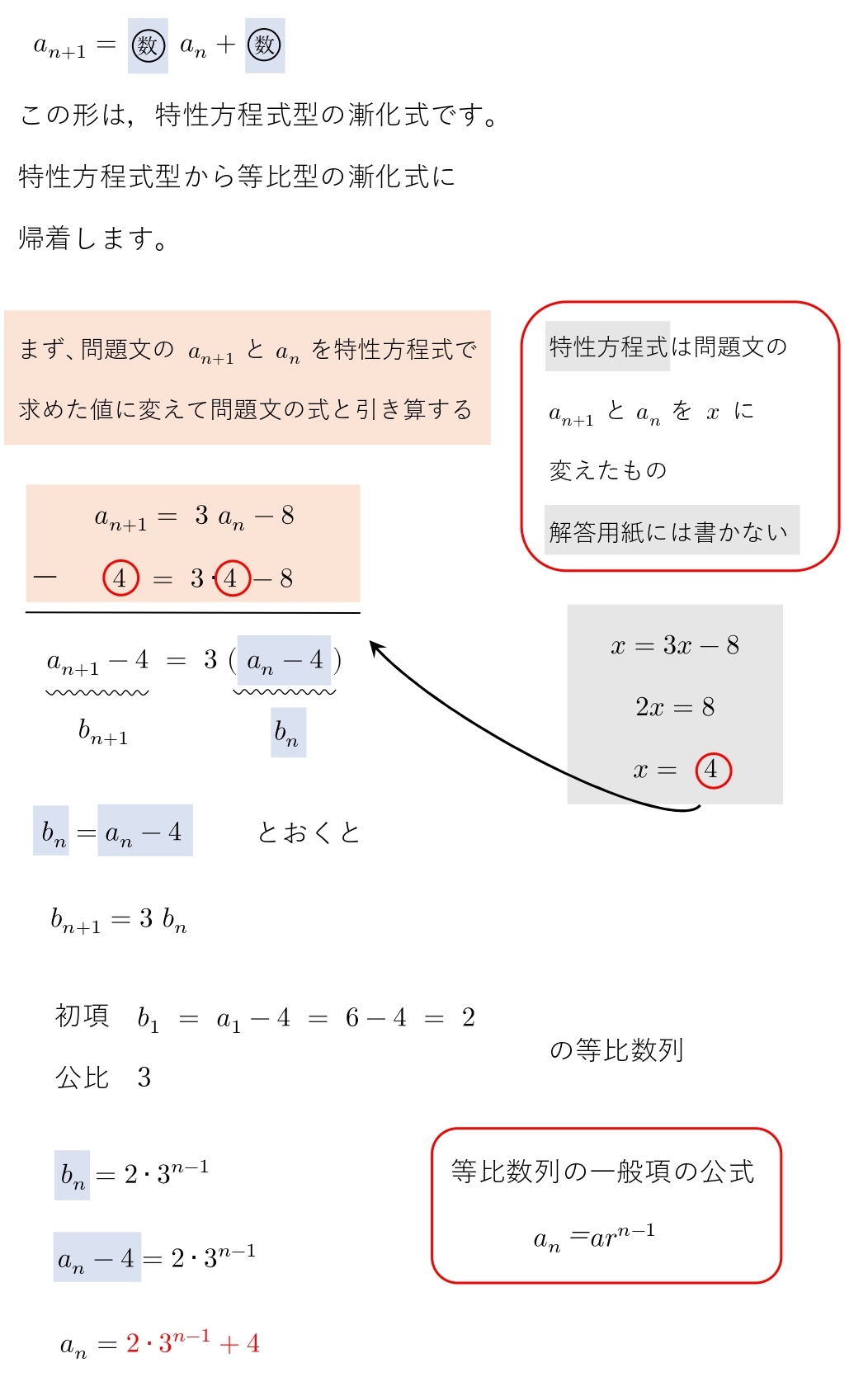
3.4 特性方程式型
特性方程式型は、等比型になる漸化式です。
\(a_1=6\),\(a_{n+1}=3a_n-8 \) によって定められる数列\({a_n}\)の一般項を求めよ。

3.5 特性階差型
特性階差型は、特性方程式型から階差型になる漸化式です。
\(a_1=1\),\(a_{n+1}=3a_n+4n \) によって定められる数列\({a_n}\)の一般項を求めよ。

\(
\hspace{ 10pt }a_{n+2}=3a_{n+1}+4(n+1) ……①\\ \\
\hspace{ 10pt }a_{n+1}=3a_n+4n \hspace{ 35pt } ……②\\ \\ \\
②-① より\\ \\
\hspace{ 10pt }a_{n+2}-a_{n+1}=3(\bbox[#DEEBF7, 2pt, border:]{a_{n+1}-a_n})+4\\ \\ \\
\bbox[#DEEBF7, 2pt, border:]{b_n}=\bbox[#DEEBF7, 2pt, border:]{a_{n+1}-a_n} とおくと\\ \\
\hspace{ 10pt } b_{n+1}=3b_n+4\hspace{ 20pt }\bbox[yellow, 2pt, border:]{特性方程式型}\\ \\
\begin{cases}
b_{n+1}+2=3(b_n+2)\\ \\
b_1+2=\bbox[#F4E2E2, 3pt, border:]{a_2}-a_1+2=\bbox[#F4E2E2, 2pt, border:]{3a_1+4}-a_1+2=8
\end{cases}\\ \\ \\
\left\{b_n+2\right\}\ は初項 \ 8,公比 \ 3 \ の等比数列なので\\ \\
\hspace{ 20pt }b_n+2=8・3^{n-1}\\ \\
\hspace{ 35pt }\bbox[#DEEBF7, 2pt, border:]{b_n}=8・3^{n-1}-2\\ \\
\bbox[#DEEBF7, 2pt, border:]{a_{n+1}-a_n}=\bbox[#E2F0D9, 2pt, border:]{8・3^{n-1}-2\ }\hspace{ 25pt }\bbox[yellow, 2pt, border:]{階差型}\\ \\ \\
n ≧ 2 のとき\\ \\
a_n = 1+ \displaystyle \sum_{k=1}^{n-1} (\bbox[#E2F0D9, 2pt, border:]{8・3^{k-1}-2\ }) \\ \\
\hspace{ 7pt } = 1+ 8\bbox[#FFF2CC, 2pt, border:]{\displaystyle \sum_{k=1}^{n-1} 3^{k-1}}-2\displaystyle \sum_{k=1}^{n-1} \\ \\
\hspace{ 7pt } = 1 +8( \bbox[#FFF2CC, 2pt, border:]{1+3^1 + 3^2 + 3^3 + \cdots + 3^{n-1}})+2(n-1) \\ \\
\hspace{ 50pt } \bbox[#FFF2CC, 2pt, border:]{初項 \ 1,公比 \ 3,項数 \ n \ の等比数列の和}\\ \\
\hspace{ 10pt } = 1+8×\bbox[#FFF2CC, 2pt, border:]{\displaystyle\frac{1・(3^n-1)}{3-1}}+2(n-1) \\ \\
\hspace{ 10pt } =4・3^{n-1}-2n-1\\ \\ \\
n = 1 のとき\\ \\
\hspace{ 10pt }a_1 = 4-2-1=1 \\ \\ \\
よって\\ \\
\hspace{ 15pt }a_n =\displaystyle \color{#ef5350}{4・3^{n-1}-2n-1}\\
\)
3.6 分数型
分数型は、特性方程式型から等比型になる漸化式です。
\(a_1= \displaystyle\frac{1}{5} \),\(a_{n+1}=\displaystyle\frac{a_n}{4a_n-1} \) によって定められる数列\({a_n}\)の一般項を求めよ。

\(
両辺に逆数をとると\\ \\
\hspace{ 10pt }\displaystyle\frac{1}{a_{n+1}}=\displaystyle\frac{4a_n-1}{a_n} \\ \\
\hspace{ 7pt }\displaystyle\frac{1}{a_{n+1}}=-\bbox[#DEEBF7, 2pt, border:]{\displaystyle\frac{1}{a_n}}+4 \\ \\ \\
\bbox[#DEEBF7, 2pt, border:]{b_n}=\bbox[#DEEBF7, 2pt, border:]{\displaystyle\frac{1}{a_n}} とおくと\\ \\
\hspace{ 10pt } b_{n+1}=-b_n+4\hspace{ 20pt }\bbox[yellow, 2pt, border:]{特性方程式型}\\ \\
\begin{cases}
b_{n+1}-2=-(b_n-2)\\ \\
\bbox[#DEEBF7, 3pt, border:]{b_1}-2=\bbox[#DEEBF7, 3pt, border:]{\displaystyle\frac{1}{a_n}}-2=5-2=3
\end{cases}\\ \\ \\
\left\{b_n-2\right\}\ は初項 \ 3,公比 \ -1 \ の等比数列なので\\ \\
\hspace{ 10pt }b_n-2=3・(-1)^{n-1}\\ \\
\hspace{ 23pt }\bbox[#DEEBF7, 2pt, border:]{b_n}=3・(-1)^{n-1}+2\\ \\
\hspace{ 20pt }\bbox[#DEEBF7, 2pt, border:]{\displaystyle\frac{1}{a_n}}=3・(-1)^{n-1}+2\\ \\
よって\\ \\
\hspace{ 15pt }a_n =\displaystyle \color{#ef5350}{\displaystyle\frac{1}{3・(-1)^{n-1}+2}}\\ \\
\)
3.7 指数型
指数型は、特性方程式型から等比型になる漸化式です。
\(a_1=3\),\(a_{n+1}=2a_n+3^{n+1} \) によって定められる数列\({a_n}\)の一般項を求めよ。

\(
両辺を\ 3^{n+1} \ で割ると\\ \\
\hspace{ 10pt }\displaystyle\frac{a_{n+1}}{3^{n+1}}=\displaystyle\frac{2a_n}{3^{n+1}}+1 \\ \\
\hspace{ 6pt }\displaystyle\frac{a_{n+1}}{3^{n+1}}=\displaystyle\frac{2}{3}・\bbox[#DEEBF7, 2pt, border:]{\frac{a_n}{3^n}}+1 \\ \\
\bbox[#DEEBF7, 2pt, border:]{b_n}=\bbox[#DEEBF7, 2pt, border:]{\displaystyle\frac{a_n}{3^n}} とおくと\\ \\
\hspace{ 10pt } b_{n+1}=\displaystyle\frac{2}{3}b_n+1\hspace{ 20pt }\bbox[yellow, 2pt, border:]{特性方程式型}\\ \\
\begin{cases}
b_{n+1}-3=\displaystyle\frac{2}{3}(b_n-3)\\ \\
\bbox[#DEEBF7, 3pt, border:]{b_1}-3=\bbox[#DEEBF7, 3pt, border:]{\displaystyle\frac{a_1}{3}}-3=1-3=-2
\end{cases}\\ \\ \\
\left\{b_n-3\right\}\ は初項 \ -2,公比\ \displaystyle\frac{2}{3} \ の等比数列なので\\ \\
\hspace{ 10pt }b_n-3=-2\displaystyle\left(\frac{2}{3}\right)^{n-1}\\ \\
\hspace{ 23pt }\bbox[#DEEBF7, 2pt, border:]{b_n}=-2\displaystyle\left(\frac{2}{3}\right)^{n-1}+3\\ \\
\hspace{ 20pt }\bbox[#DEEBF7, 2pt, border:]{\displaystyle\frac{a_n}{3^n}}=-2\displaystyle\left(\frac{2}{3}\right)^{n-1}+3 \\ \\
よって\\ \\
\hspace{ 15pt }a_n =3^n\left\{-2\displaystyle\left(\frac{2}{3}\right)^{n-1}+3\right\}\\ \\
\hspace{ 25pt } =\displaystyle \color{#ef5350}{-3・2^n+3^{n+1}}\\ \\
\)
3.8 対数型
対数型は、特性方程式型から等比型になる漸化式です。
\(a_1=1\),\(a_{n+1}=2\sqrt{a_n} \) によって定められる数列\({a_n}\)の一般項を求めよ。

\(
両辺に\ \log_2 \ をとると\\ \\
\hspace{ 10pt }\log_2{a_{n+1}}=\log_2{2\sqrt{a_n}} \\ \\
\hspace{ 10pt }\log_2{a_{n+1}}=\log_2{2}+\log_2{\sqrt{a_n}} \\ \\
\hspace{ 10pt }\log_2{a_{n+1}}=\displaystyle\frac{1}{2}\bbox[#DEEBF7, 2pt, border:]{\log_2{a_n}}+1 \\ \\
\bbox[#DEEBF7, 2pt, border:]{b_n}=\bbox[#DEEBF7, 2pt, border:]{\log_2{a_n}} とおくと\\ \\
\hspace{ 10pt } b_{n+1}=\displaystyle\frac{1}{2}b_n+1\hspace{ 20pt }\bbox[yellow, 2pt, border:]{特性方程式型}\\ \\
\begin{cases}
b_{n+1}-2=\displaystyle\frac{1}{2}(b_n-2)\\ \\
\bbox[#DEEBF7, 3pt, border:]{b_1}-2=\bbox[#DEEBF7, 3pt, border:]{\log_2{1}}-2=0-2=-2
\end{cases}\\ \\ \\
\left\{b_n-2\right\}\ は初項 \ -2,公比\ \displaystyle\frac{1}{2} \ の等比数列なので\\ \\
\hspace{ 10pt }b_n-2=-2\displaystyle\left(\frac{1}{2}\right)^{n-1}\\ \\
\hspace{ 20pt }b_n=2-2・2^{1-n}\\ \\
\hspace{ 20pt }\bbox[#DEEBF7, 2pt, border:]{b_n}=2-2^{2-n}\\ \\
\hspace{ 20pt }\bbox[#DEEBF7, 2pt, border:]{\log_2{a_n}}=2-2^{2-n} \\ \\
よって\\ \\
\hspace{ 15pt }a_n =\color{#ef5350}{2^{2-2^{2-n}}}\\ \\
\)
3.9 階比型
階比型は、 \(a_1\) になるまで漸化式を繰り返して解きます。
\(a_1=3\),\((n+1)a_{n}=(n-1)a_{n-1} \ \ \ (n≧2)\) によって定められる数列\({a_n}\)の一般項を求めよ。

\(
\hspace{ 10pt }a_{n}=\displaystyle\frac{n-1}{n+1}\ \bbox[#F4E2E2, 3pt, border:]{a_{n-1}} \\ \\
\hspace{ 25pt }=\displaystyle\frac{n-1}{n+1}・\bbox[#F4E2E2, 3pt, border:]{\frac{n-2}{n}\ \bbox[#DEEBF7, 2pt, border:]{a_{n-2}}} \\ \\
\hspace{ 25pt }=\displaystyle\frac{n-1}{n+1}・\frac{n-2}{n}・\bbox[#DEEBF7, 2pt, border:]{\frac{n-3}{n-1}\ a_{n-3}} \\ \\
\hspace{ 25pt }=\displaystyle\frac{\require{cancel}\bcancel{n-1}}{n+1}・\frac{\require{cancel}\bcancel{n-2}}{n}・\frac{\require{cancel}\bcancel{n-3}}{\require{cancel}\bcancel{n-1}}・…・\frac{\require{cancel}\bcancel{3}}{\require{cancel}\bcancel{5}}・\frac{2}{\require{cancel}\bcancel{4}}・\frac{1}{\require{cancel}\bcancel{3}}・\bbox[#E2F0D9, 2pt, border:]{a_1} \\ \\
\hspace{ 25pt }=\displaystyle\frac{2}{n(n+1)}・\ \bbox[#E2F0D9, 2pt, border:]{3} \\ \\
\hspace{ 25pt }=\color{#ef5350}{\displaystyle\frac{6}{n(n+1)}}
\)
3.10 部分分数分解型
部分分数分解型は、階差型から部分分数分解していく漸化式です。
\(a_1=2\),\(a_{n+1}=\displaystyle\frac{n+2}{n}a_n+1 \) によって定められる数列\({a_n}\)の一般項を求めよ。

\(
両辺を\ \displaystyle\frac{1}{(n+1)(n+2)}\ でわると\\ \\
\hspace{ 10pt }\displaystyle\frac{a_{n+1}}{(n+1)(n+2)}=\bbox[#DEEBF7, 2pt, border:]{\frac{a_n}{n(n+1)}}+\frac{1}{(n+1)(n+2)} \\ \\
\bbox[#DEEBF7, 2pt, border:]{b_n}=\bbox[#DEEBF7, 2pt, border:]{\displaystyle\frac{a_n}{n(n+1)}} とおくと\\ \\
\hspace{ 10pt } b_{n+1}=b_n+\displaystyle\frac{1}{(n+1)(n+2)}\hspace{ 20pt }\bbox[yellow, 2pt, border:]{階差型}\\ \\
\hspace{ 10pt }\bbox[#DEEBF7, 3pt, border:]{b_1}=\bbox[#DEEBF7, 3pt, border:]{\displaystyle\frac{a_1}{1・2}}=\displaystyle\frac{2}{2}=1\\ \\
n ≧ 2 のとき\\ \\
\hspace{ 10pt }b_n = 1+ \displaystyle \sum_{k=1}^{n-1} \frac{1}{(k+1)(k+2)} \\ \\
\hspace{ 22pt } = 1+ \displaystyle \sum_{k=1}^{n-1} \left(\frac{1}{k+1}-\frac{1}{k+2} \right)\\ \\
\hspace{ 22pt } =1+\left\{\displaystyle \left( \frac{1}{2}-\frac{1}{3}\right) + \left( \frac{1}{3}-\frac{1}{4}\right) + \left( \frac{1}{n}-\frac{1}{n+1}\right) \right\} \\ \\
\hspace{ 22pt } = 1 + \displaystyle\frac{1}{2}-\frac{1}{n+1} \\ \\
\hspace{ 22pt } = \displaystyle \frac{3n+1}{2(n+1)}\\ \\ \\
n = 1 のとき\\ \\
\hspace{ 10pt }b_1 = \displaystyle\frac{4}{2・2} =1\\ \\ \\
よって\\ \\
\hspace{ 33pt } \bbox[#DEEBF7, 2pt, border:]{b_n}= \displaystyle \frac{3n+1}{2(n+1)}\\ \\
\hspace{ 5pt } \displaystyle\frac{a_n}{n(n+1)}= \displaystyle \frac{3n+1}{2(n+1)}\\ \\
\hspace{ 35pt }a_n =\displaystyle \color{#ef5350}{\displaystyle{\frac{n(3n+1)}{2}}}\\
\)
4. まとめ
漸化式の問題では
① どのパターンか見分ける
② 初手を覚える
この2点が重要です。
漸化式は苦手な人が多い分野なので、公式と解法をしっかり覚えて周りと差をつけよう。
「漸化式」の公式を、PDFファイルでA4プリント1枚にまとめました。

漸化式のフローチャートを、PDFファイルでA4プリント1枚にまとめました。