このページでは、「ドラえもんの四次元ポケット」を具体的にわかりやすく説明していきます。
また、0次元・1次元・2次元・3次元・4次元のイメージを数学と物理学から解説します。
少しでも数学に興味を持てるきっかけになれば嬉しいです。

[toc]
1. 四次元ポケットとは
見た目は半円形の白い袋。
ポケットの中は四次元空間(超空間)に繋がっており、そこは大きさも重さも関係ない世界なので、ものを無限に収納することができる。
それでは、四次元ポケットとはなにか考えてみましょう。
2. 数学的な4次元とは
2.1 1次元、2次元、3次元
まずは、1次元、2次元、3次元を考えてみます。

1次元は、線
2次元は、平面
3次元は、空間
のことです。
次は、0次元を考えてみます。
2.2 0次元
3次元から考えてみましょう。

空間(3次元)は、平面(2次元)の集合です。
平面(2次元)は、線(1次元)の集合です。
線(1次元)は、点(0次元)の集合です。
よって、0次元は点です。
2.3 数学的な4次元
次に、数学的に4次元について考えていきます。
0次元から考えていくと
1次元(線)は、0次元(点)を収納できます。
2次元(平面)は、1次元(線)を収納できます。
3次元(空間)は、2次元(平面)を収納できます。
では、4次元とは何でしょうか?
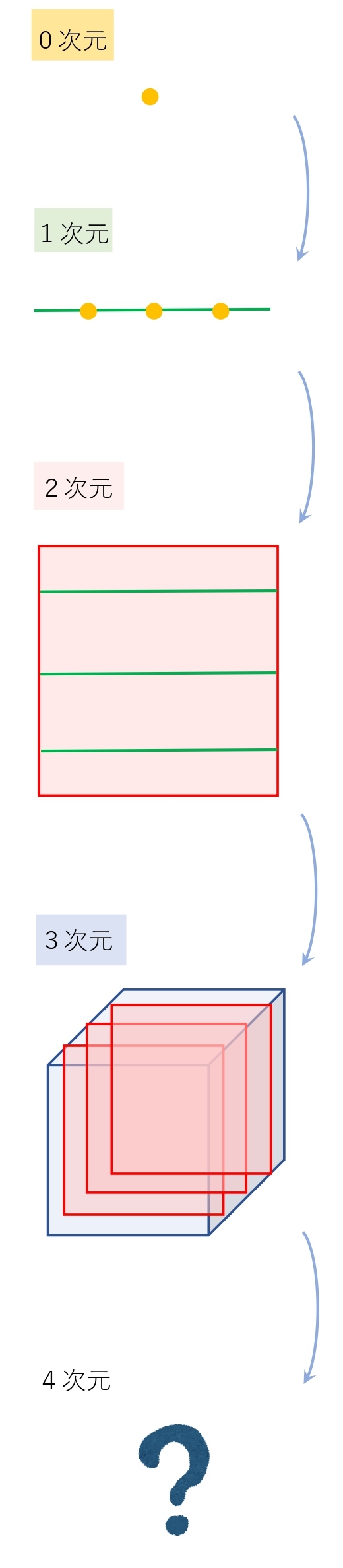
4次元は3次元(空間)を収納できると考えることができます。
2.4 四次元ポケットの意味
それでは、四次元ポケットとは何でしょうか。
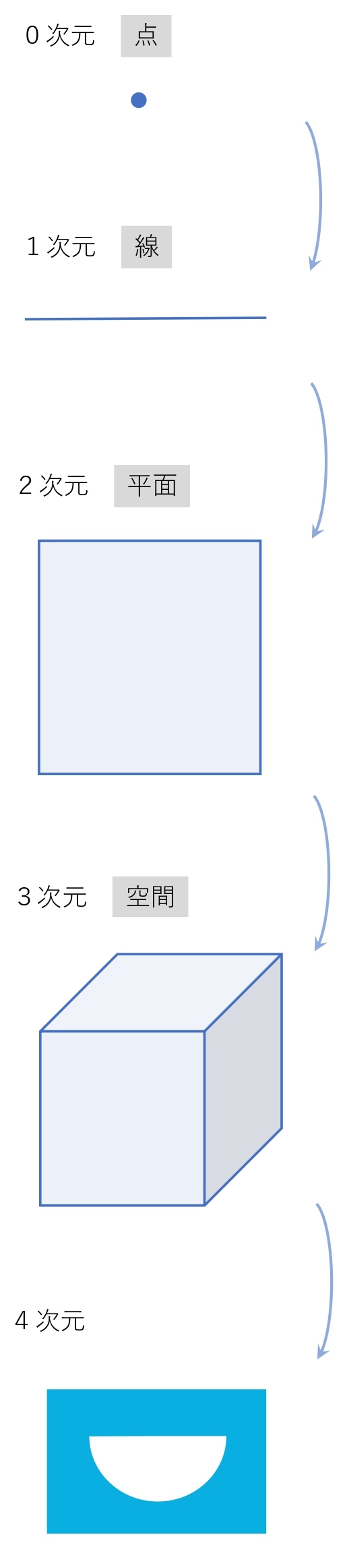
「四次元ポケット」は「3次元空間を収納できるポケット」ということになります。
ものを無限に収納できるということです。
3. 物理学的な4次元とは
3.1 座標軸の本数と次元
続いて、物理学の視点から4次元を考えてみます。
座標軸の本数に着目して、次元を定義してみると…
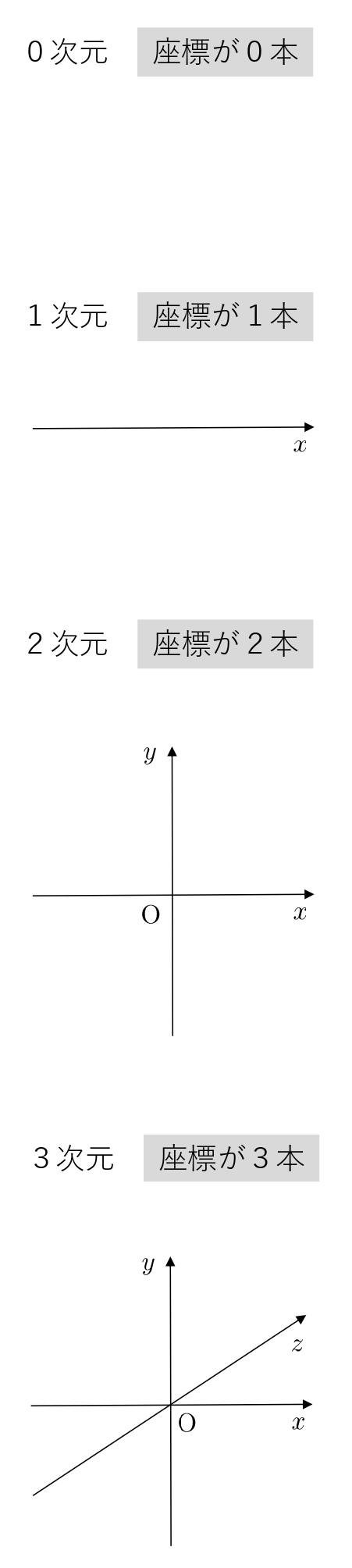
0次元 → 軸0本
1次元 → \(x\) 軸の1本
2次元 → \(x\) 軸,\(y\) 軸の2本
3次元 → \(x\) 軸,\(y\) 軸,\(z\) 軸の3本
軸の本数が増えると、次元も増えていきます。
3.2 物理学的な4次元
次元が、座標軸の本数に対応しているのならば
4次元 → 座標軸4本ということになります。
\(x\ 軸,y\ 軸,z\) 軸に、時間軸の \(t\) 軸を1本増やしてみましょう。
( \(t\) は \(time\) の \(t\) です)
4次元 → \(x\) 軸,\(y\) 軸,\(z\) 軸,\(t\) 軸の4本
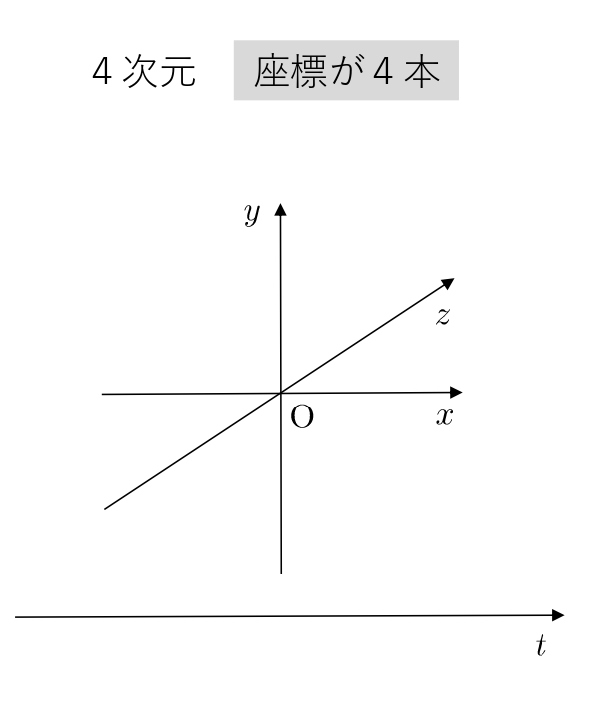
\(x\) 軸,\(y\) 軸,\(z\) 軸が、時間軸の \(t\) 軸上を動くということは、次のように表すことができます。
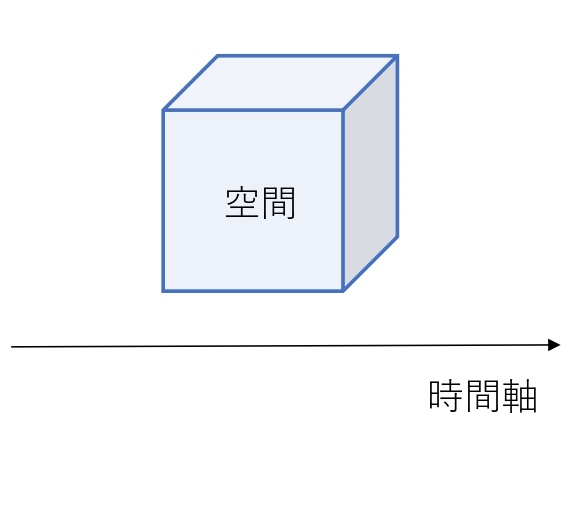
時間軸は、過去から未来に進むので、3次元空間が過去から未来に動きます。
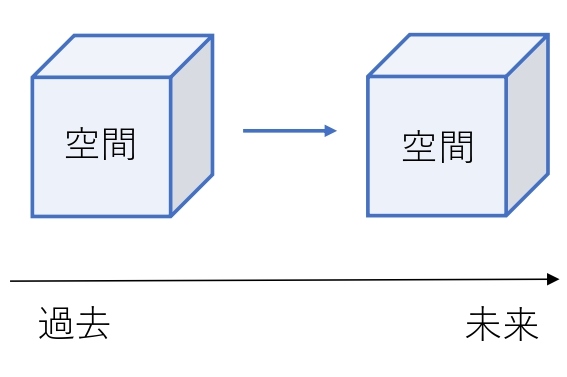
つまり…

タイムマシンのことです。
4. のび太くんの部屋の秘密
のび太くんの部屋には四次元ポケットとタイムマシンがあります。
のび太くんの部屋には
数学的な四次元
物理学的な四次元
2つの四次元が描かれているのです。
あくまでイメージなので、厳密ではありません。
数学に興味をもつきっかけになれば嬉しいです。
