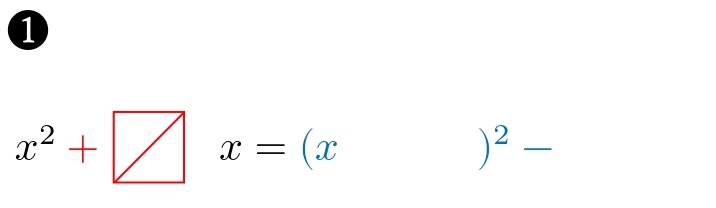このページでは、数学Ⅰ「平方完成」をまとめました。
平方完成の公式と計算方法を、具体的に問題を解きながらわかりやすく解説していきます。
問題集を解く際の参考にしてください!
 [toc]
[toc]
1. 平方完成の公式
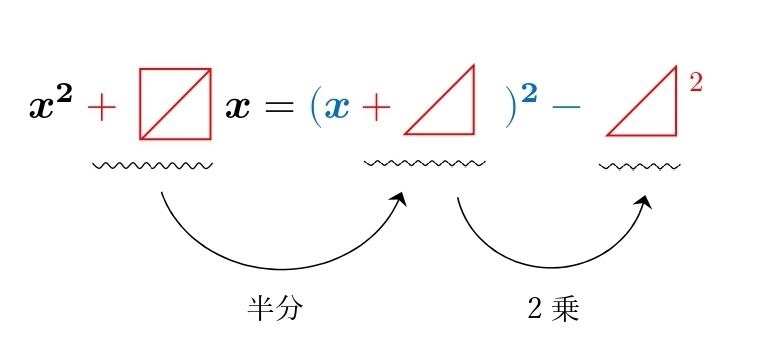
2. 平方完成のやり方
\( (x )^2- \) を書きます。
この形は、毎回同じなので最初に書きます。
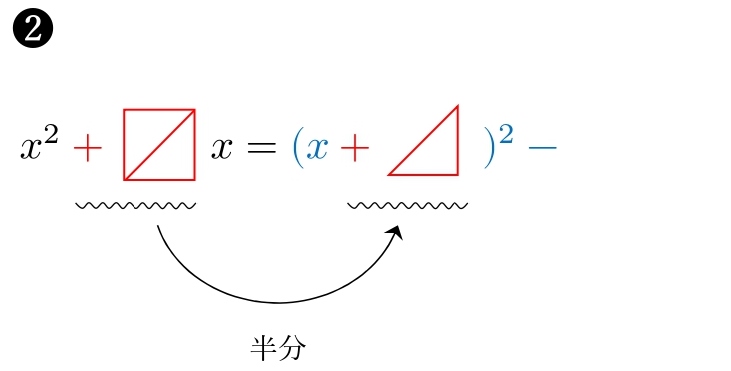
左側のスペースに、![]() の半分を入れます。
の半分を入れます。
\( 2 \) なら \( 1 \) \( -4 \) なら \( -2 \) \( 3 \) なら \( \displaystyle \frac{3}{2} \)
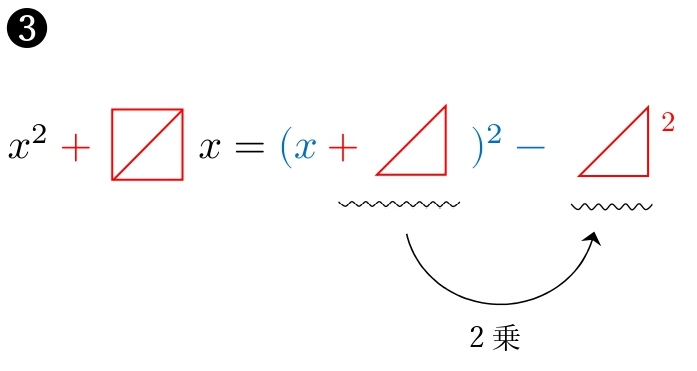
右側のスペースに、先程半分にしたものの \( 2 \) 乗を入れます。
\( 1 \) なら \( 1 \) \( -2 \) なら \( 4 \) \( \displaystyle \frac{3}{2} \) なら \( \displaystyle \frac{9}{4} \)
以上が、平方完成のやり方になります。
次に、実際に平方完成していきます。
3. 平方完成の問題解説
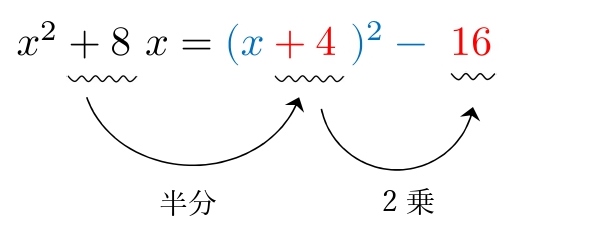
3.1 \( x^2+△x \)
\( x^2+8x \) を平方完成せよ。
3.2 \( x^2+△x+□ \)
\( x^2-6x+8 \) を平方完成せよ。
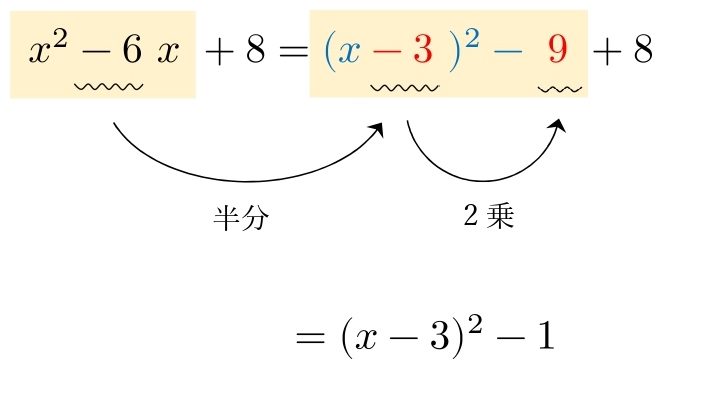
\( -6 \) の半分は \( -3 \)
\( -3 \) の2乗は \( 9 \)
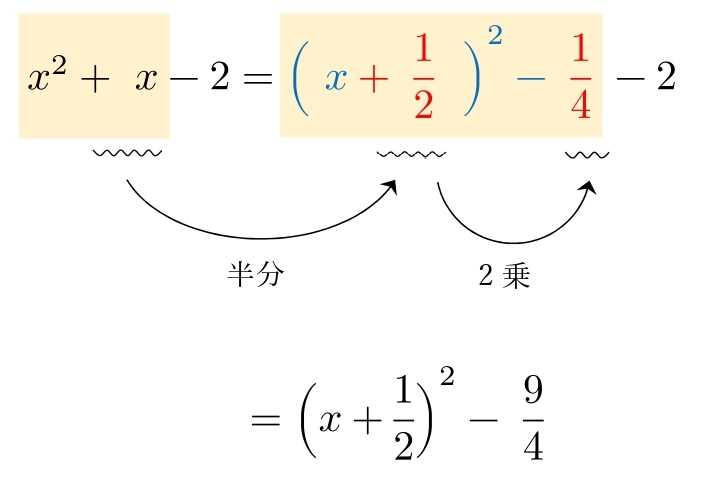
3.3 \( x^2+△x+□ \)(分数型)
\( x^2+x-2 \) を平方完成せよ。
3.4 \( ○x^2+△x+□ \)
\( 2x^2+4x+5 \) を平方完成せよ。
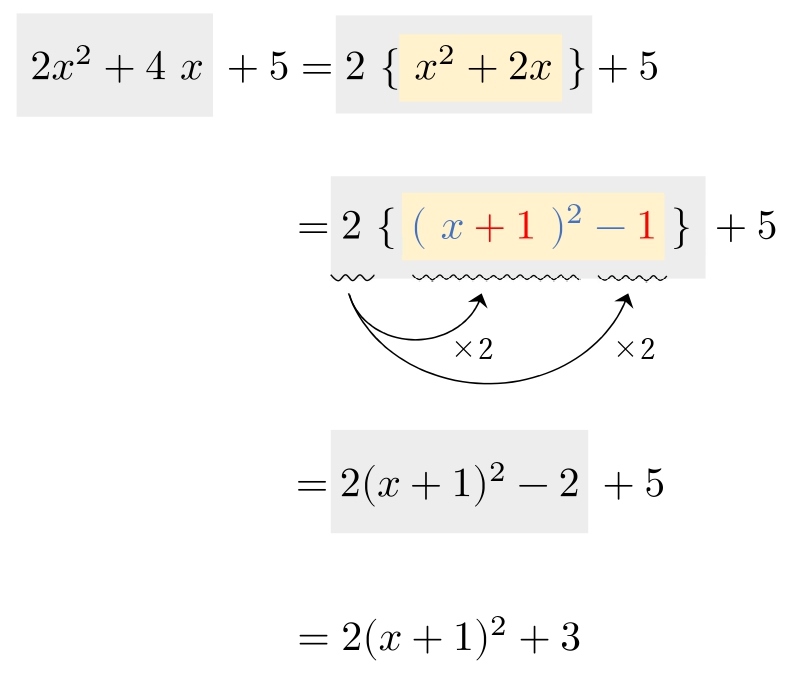
3.5 \( ○x^2+△x+□ \)(分数型)
\( -2x^2+6x+4 \) を平方完成せよ。
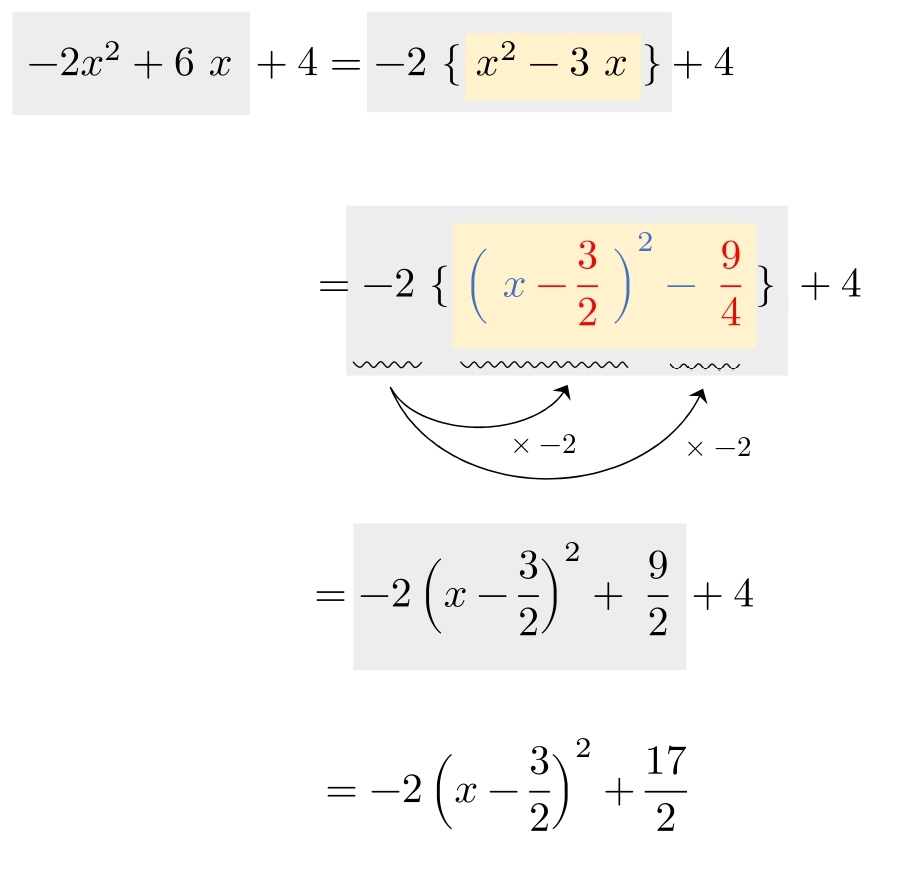
以上が平方完成の 5 パターンの解説です。
まずは基礎パターンをおさえて,すべてのパターンを使いこなせるようにしましょう。
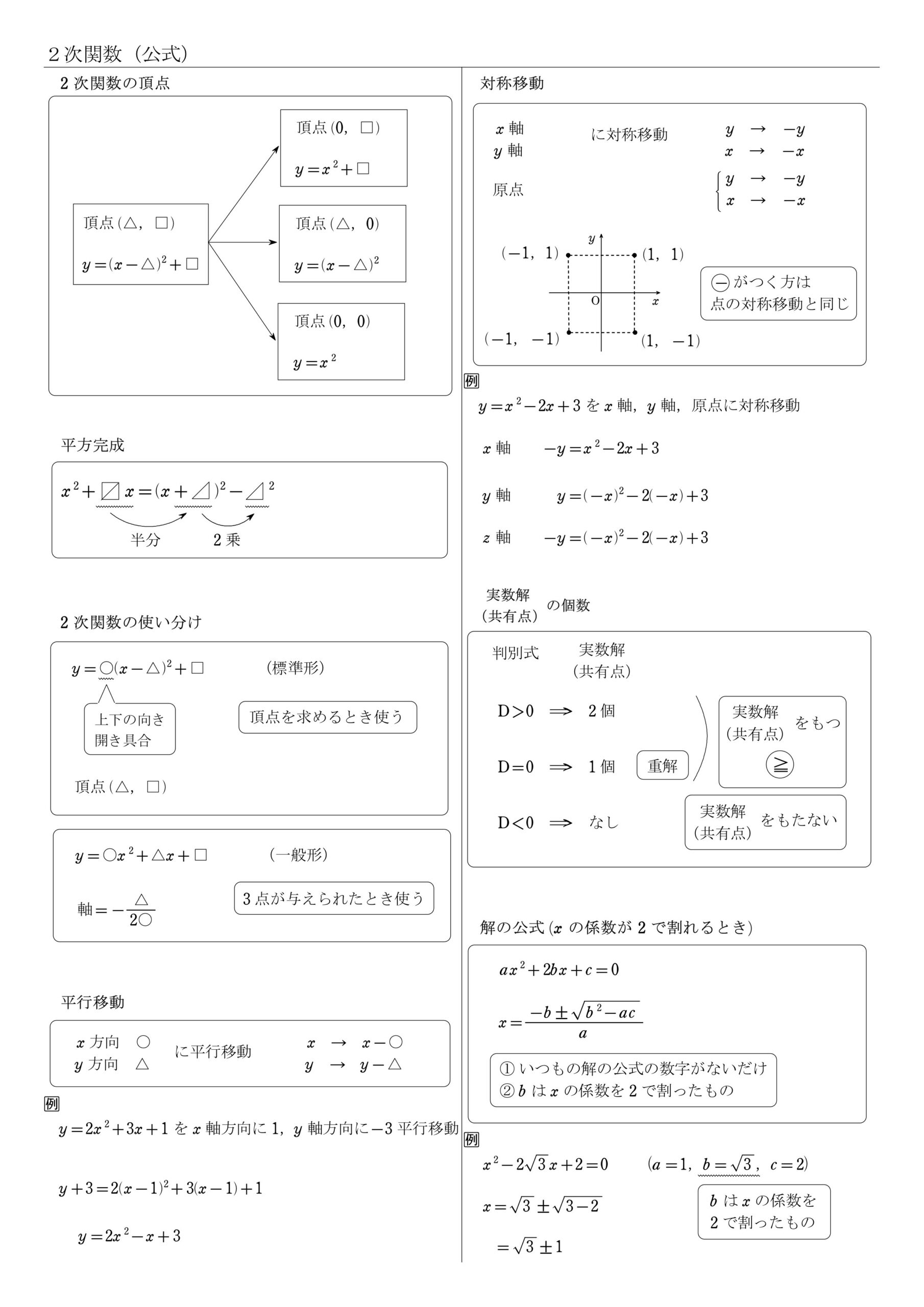
4. 公式まとめ
数学Ⅰ「2次関数」の公式を、PDFファイルでA4プリント1枚にまとめました。
5. 平方完成の問題一覧
数学Ⅰ「2次関数」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
ぜひチェックしてみてください。
このページでは、数学Ⅰ「ʌ ...

【高校数学Ⅰ】2次関数 教科書(問題・解答・公式・解説)