このページでは、「2=1の証明」について解説しています。
0で割れない理由を、具体的にわかりやすく解説していきます。
少しでも数学に興味を持てるきっかけになれば嬉しいです。

1. 2=1 の証明
\(2=1\) を証明せよ。

有名な証明問題です。
どこが違っているのかわかりますか?
正解は、「④ 両辺を \(a-b\) で割る」です。
なぜなら、\(a=b\) と仮定しているので \(a-b=0\) です。
数学は 0 で割ってはいけないのです。
この証明問題は、2008年に虚構新聞に掲載された記事です。
虚構新聞なので嘘の記事ですが、よくできた証明問題ですね。
それでは、なぜ 0 で割ってはいけないのか考えてみましょう。
2. 0で割ってはいけない理由(中学生向け)
\( 4÷2=2 \hspace{25pt } ⇒ \hspace{25pt } 4=2×2\\ \\
6÷2=3\hspace{25pt }⇒\hspace{25pt }6=3×2\)
このように割り算は、掛け算で表すことができます。
それでは
\( \bbox[#D9D9D9, 2pt, border:]{3÷0=x} \)
を考えてみましょう。
0 で割ると何になるかわからないので、\(x\) とします。
同じように割り算を掛け算に変換すると
\( 3÷0=x \hspace{25pt } ⇒ \hspace{25pt } 3=x×0\)
\(\hspace{107pt }\color{#ef5350}{3=0}\)
\(3=0\) になって矛盾します。
3. 0で割ってはいけない理由(高校生向け)
\( 1÷2 \hspace{25pt } ⇒ \hspace{25pt } \displaystyle{\frac{1}{2}}\\ \\
1÷3\hspace{25pt }⇒\hspace{25pt }\displaystyle{\frac{1}{3}}\)
のように割り算は分数で表すことができます。
0 で割ってはいけないということは、分母が 0 になってはいけないと言い換えることができます。
それでは
\( \bbox[#D9D9D9, 2pt, border:]{1÷0} \)
を考えてみましょう。
例えば、\(y=\displaystyle{\frac{1}{x}}\) のグラフを考えてみます。
数Ⅲ
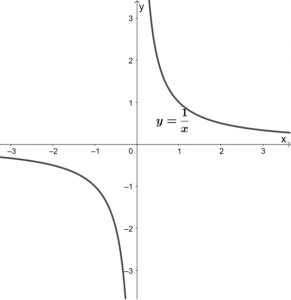

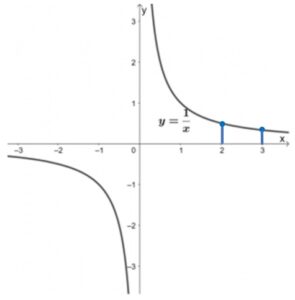
それでは、\(x=0\) のときはどうなるでしょう。グラフを見てください。
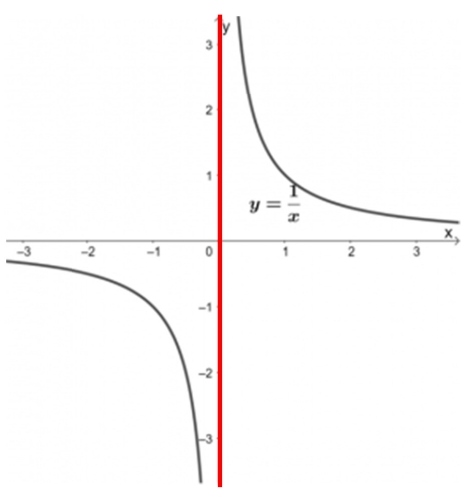
\(x=0\) は存在しないのです。
4. 問題を解くときに気を付けること
0 で割ってはいけないことがわかりましたか?
数式を見たときは、常に 0 の可能性を考えなければいけません。
高校数学の分野でいくつか例を出します。
例えば、
\( \bbox[#D9D9D9, 2pt, border:]{\displaystyle{\frac{x^2+3x+2}{a-1}=3}} \)
という \( x \) の方程式を見たときに、すぐに \( \bbox[#D9D9D9, 2pt, border:]{a≠1} \) という条件が思いつかなければいけません。
例えば、
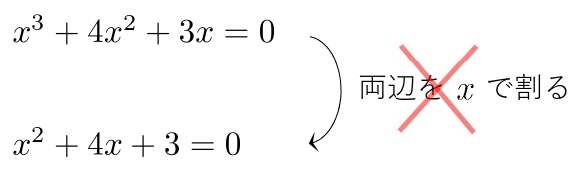
としてはいけません。
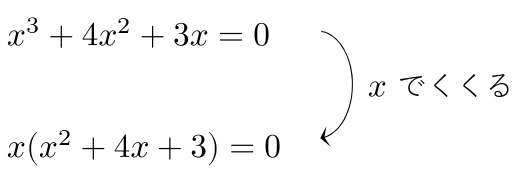
\( x=0 \) の可能性があるので、 \(x\) でくくらなければいけません。
0 の可能性は常に意識しましょう。
