このページでは、数学Ⅰ「展開・因数分解の公式」について、まとめています。
展開・因数分解の公式と計算方法を，具体的に問題を解きながらわかりやすく解説していきます。
問題集を解く際の参考にしてください！
1. 展開
1.1 ２次式の展開
\( (a+2b-c)^2 \) を展開せよ。
\( (a+2b\bbox[#DEEBF7, 2pt, border:]{-c})^2 \\ \\
=(a+2b\bbox[#DEEBF7, 2pt, border:]{+(-c)})^2\\ \\
=\color{#ef5350}{a^2+4b^2+c^2+4ab-4bc-2ac} \\ \)
\(-\) のときは \(+\) に変換して解けば、覚える公式は \(+\) のときの１つで済みます。
1.2 ３次式の展開
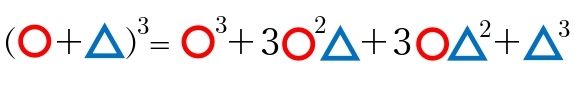
は左から 3乗、2乗、1乗、0乗
は左から 0乗、1乗、2乗、3乗 になっています。
\(
次の式を展開せよ。\\ \\
(1) (3a+b)^3 \\ \\
(2) (x-2y)^3\\
\)
\( (3a+b)^3 \\ \\
=(3a)^3+3(3a)^2(b)+3(3a)(b)^2+(b)^3 \\ \\
=\color{#ef5350}{27a^3+27a^2b+9ab^2+b^3} \\ \)
\( (x\bbox[#DEEBF7, 2pt, border:]{-2y})^3 \\ \\
=(x\bbox[#DEEBF7, 2pt, border:]{+(-2y)})^3 \\ \\
=x^3+3x^2(-2y)+3x(-2y)^2+(-2y)^3 \\ \\
=\color{#ef5350}{x^3-6x^2y+12xy^2-8y^3} \\ \)
\(-\) のときは \(+\) に変換して解きます。
2. 因数分解
2.1 ３次式の因数分解
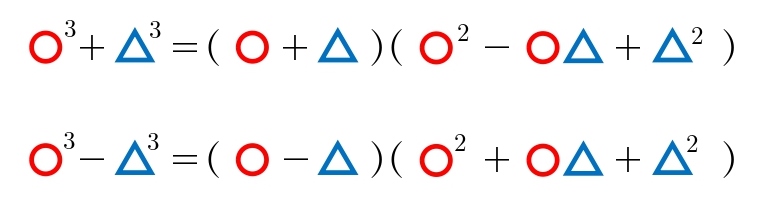
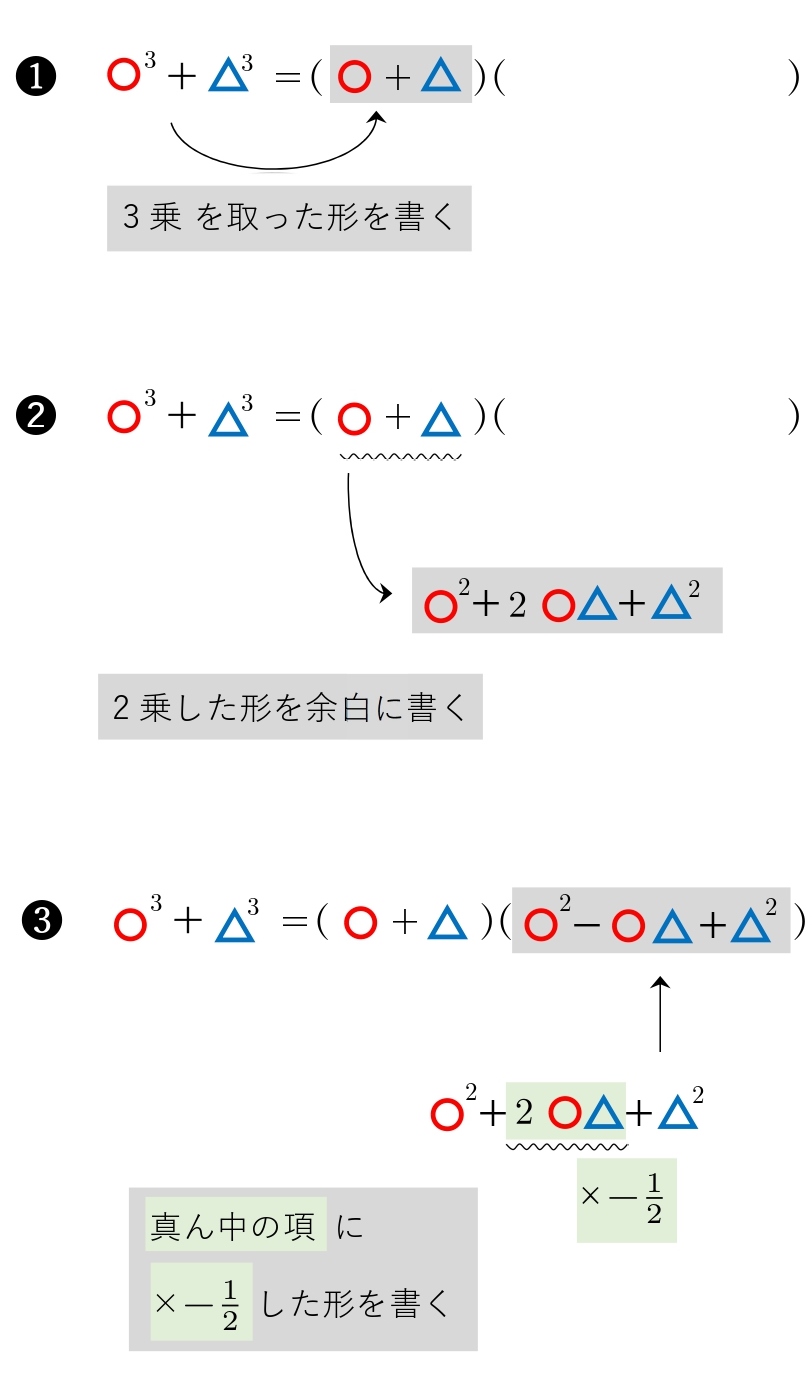
\(-\) のときもやり方は同じです。
やり方がわかったら、実際に問題を解いてみましょう。
\(
次の式を因数分解せよ。\\ \\
(1) x^3-1 \\ \\
(2) x^3+27a^3\\
\)
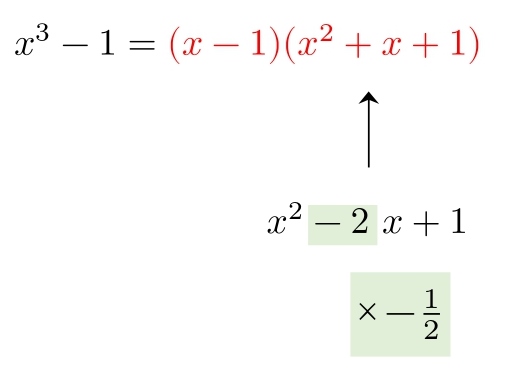
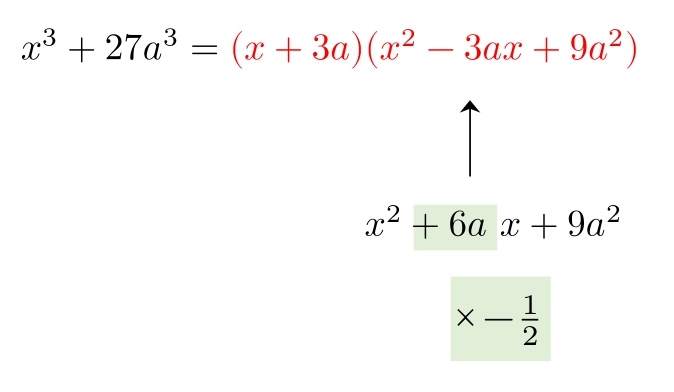
3. 公式まとめ
数学Ⅰ「数と式」で使う公式をPDF（A4）にまとめました。
4. 展開・因数分解の問題
数学Ⅰ「展開・因数分解の公式」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
