このページでは、数学Ⅱの「組立除法のやり方と計算方法」についてまとめています。
組立除法の計算方法を,具体的に問題を解きながらわかりやすく解説していきます。
問題集を解く際の参考にしてください!
[toc]
1. 組立除法とは
組立除法とは、多項式を一次式で割って商と余りを出す方法。
2. 組立除法のやり方
例題を使って、組立除法のやり方を解説していきます。
\(x^3-4x^2+x+6\) を \( x-2 \) で割った商と余りを求めよ。



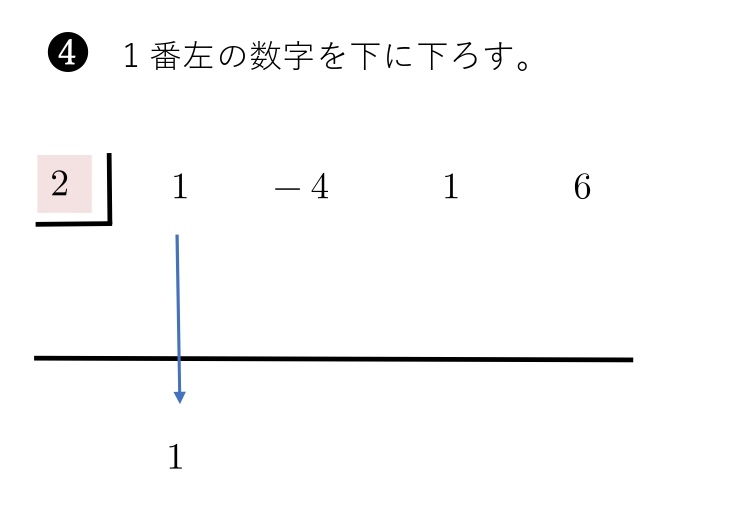
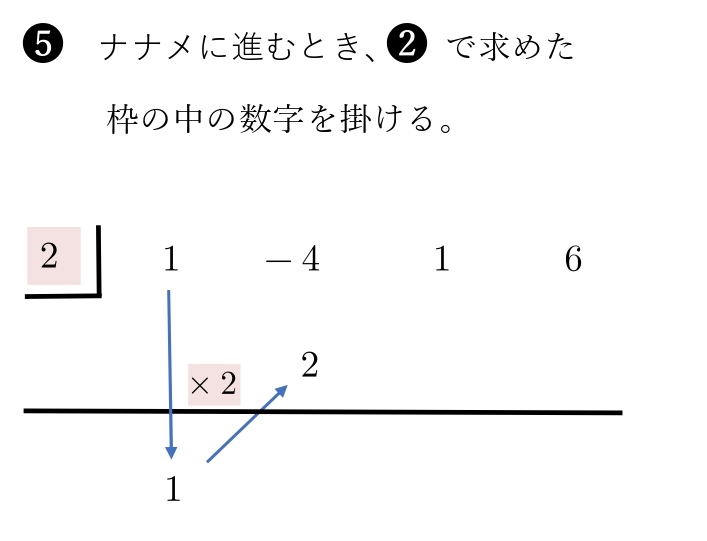

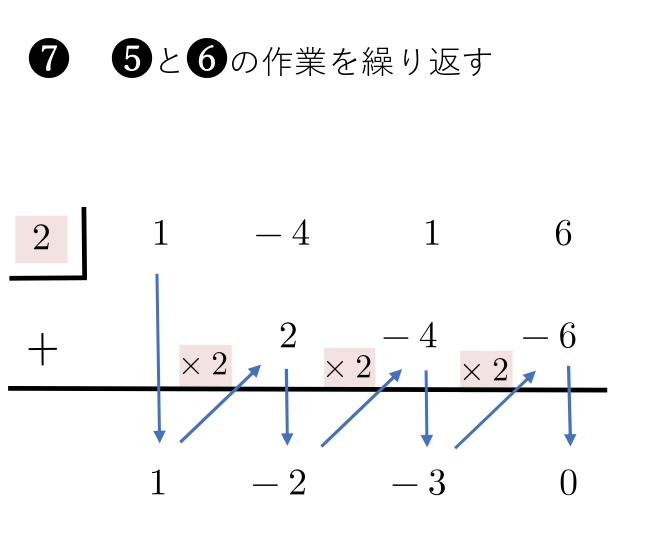
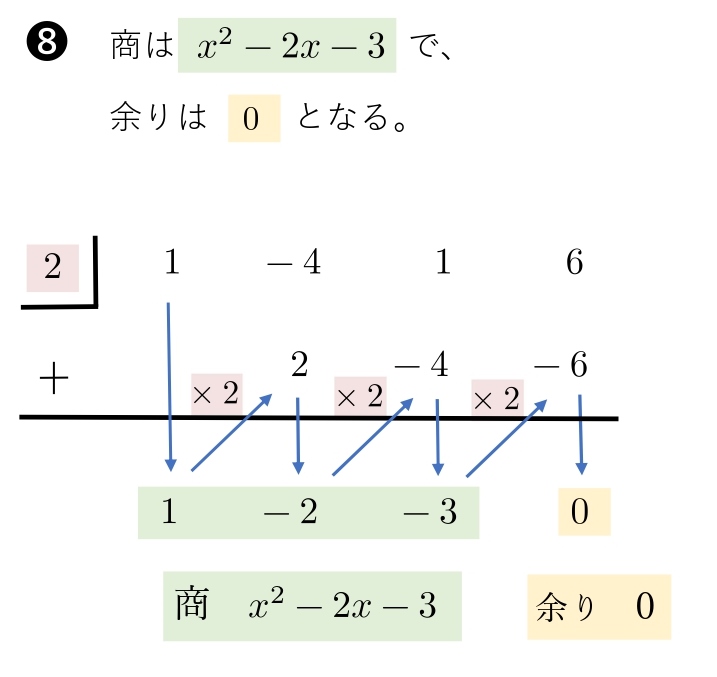
\(1,-2,\ \ 3\) は, \(x^2\) の係数,\(x\) の係数,定数を表しています。
3. 組立除法の問題
\(x^3-x+2=0\) を \( x-2 \) で割った商と余りを求めよ。
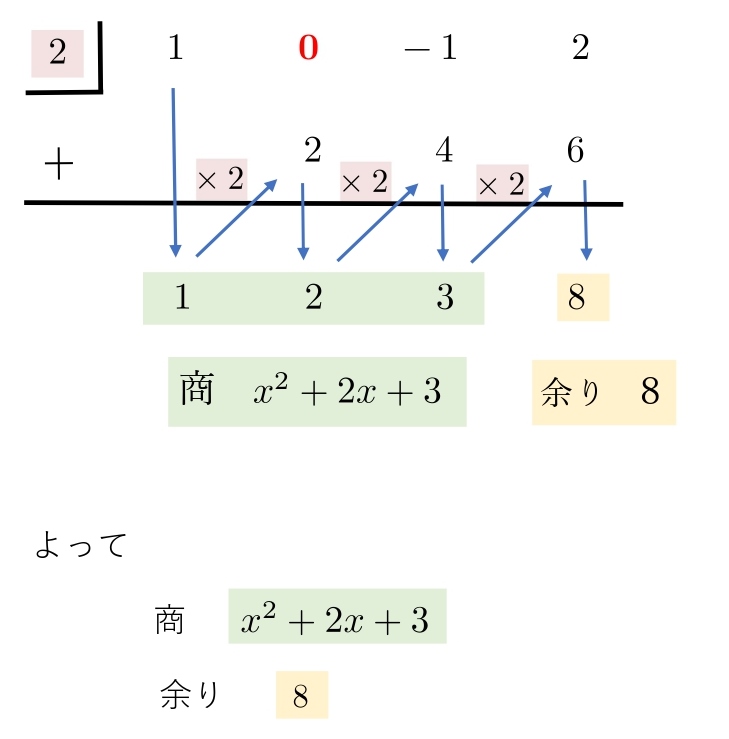
\(x^3-x+2=0\) のように \(x^2\) の項がないときは0として扱います。
以上が、組立除法のやり方と計算方法です。
組立除法は「3次方程式を解くとき」と「整式の除法で商と余りを求めるとき」に使います。こちらのページで詳しく説明しているので、チェックしてみてください。
このページでは、数学Ⅱの{ ... このページでは、数学Ⅱの{ ...

【高校数学Ⅱ】高次方程式 解き方一覧(因数分解・置換・組立除法)

【高校数学Ⅱ】整式の除法による余りの求め方(筆算・剰余の定理・組立除法)
4. 公式まとめ
数学Ⅱ「複素数と方程式」の公式を、PDFファイルでA4プリント1枚にまとめました。
5. 組立除法の問題
数学Ⅱ「複素数と方程式」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
ぜひチェックしてみてください。
このページでは、数学Ⅱ「Ş ...
【高校数学Ⅱ】複素数と方程式 教科書(問題・解答・公式・解説)

