このページでは、数学Ⅱの「高次方程式の解き方」についてまとめています。
高次方程式とは、3次以上の方程式のことです。
ここでは、3次方程式、4次方程式を扱います。
高次方程式の解き方は、因数分解、置換、組立除法の3パターンあります。
それぞれの公式や計算方法を,具体的に問題を解きながらわかりやすく解説していきます。
問題集を解く際の参考にしてください!
[toc]
1. 高次方程式の解き方
1.1 因数分解
\(
次の方程式を解け。\\ \\
\hspace{ 10pt }x^3=8\\
\)
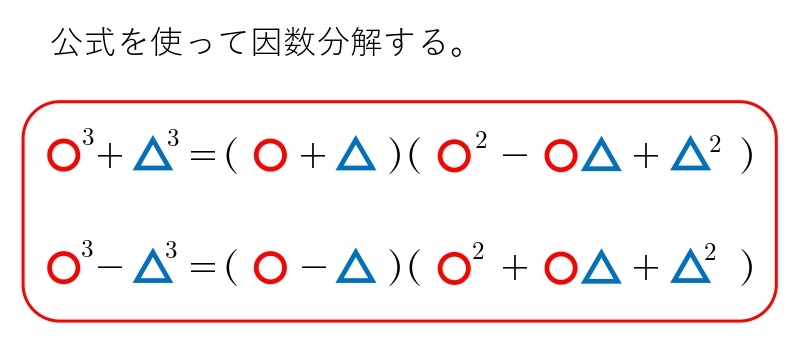
\(x^3=8\\ \\
\bbox[#DEEBF7, 2pt, border:]{x^3-8}=0\\ \\
\bbox[#DEEBF7, 2pt, border:]{(x-2)(x^2+2x+4)}=0\\ \\ \\
x-2=0\hspace{ 10pt }のとき\\ \\
\hspace{ 20pt }x=2\\ \\ \\
x^2+2x+4=0\hspace{ 10pt }のとき\\ \\
\hspace{ 20pt }x=\displaystyle\frac{-2\pm\sqrt{ 4-16 }}{2}\\ \\
\hspace{ 20pt }x=\displaystyle\frac{-2\pm2\sqrt{ 3 }\ i}{2}\\ \\
\hspace{ 20pt }x=-1+\sqrt{ 3 }\ i\\ \\ \\
よって\\
\hspace{ 20pt }\color{#ef5350}{x=2,-1+\sqrt{ 3 }\ i}\\ \)
1.2 置き換え
\(
次の方程式を解け。\\ \\
\hspace{ 10pt }x^4+x^2-12=0\\
\)

\(x^4+x^2-12=0\\ \\
(\bbox[#DEEBF7, 2pt, border:]{x^2})^2+\bbox[#DEEBF7, 2pt, border:]{x^2}-12=0\\ \\
\bbox[#DEEBF7, 2pt, border:]{x^2}=\bbox[#F4E2E2, 2pt, border:]{A}\hspace{ 10pt }とおく\\ \\
\bbox[#F4E2E2, 2pt, border:]{A}^2+\bbox[#F4E2E2, 2pt, border:]{A}-12=0\\ \\
(A+4)(A-3)=0\\ \\
\hspace{ 10pt }\bbox[#F4E2E2, 2pt, border:]{A}=-4,3\\ \\
\hspace{ 10pt }\bbox[#DEEBF7, 2pt, border:]{x^2}=-4,3\\ \\ \\
x^2=-4\hspace{ 10pt }のとき\\ \\
\hspace{ 10pt }x=\pm\sqrt{-4}\\ \\
\hspace{ 10pt }x=\pm\sqrt{4}\ i\\ \\
\hspace{ 10pt }x=\pm2\ i\\ \\ \\
x^2=3\hspace{ 10pt }のとき\\ \\
\hspace{ 10pt }x=\pm\sqrt{3}\\ \\
よって\\
\hspace{ 20pt }\color{#ef5350}{x=\pm2\ i,\pm\sqrt{ 3 }} \\ \)
1.3 組立除法
\(
次の方程式を解け。\\ \\
\hspace{ 10pt }x^3-4x^2+x+6=0\\
\)
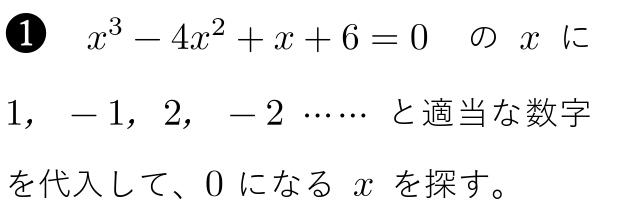


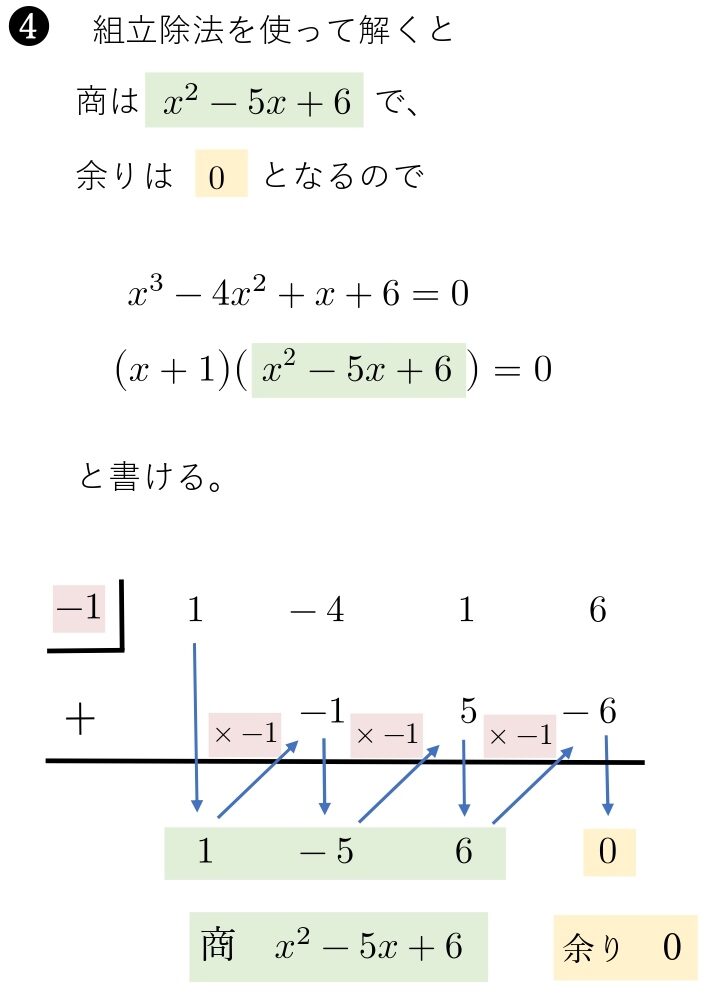
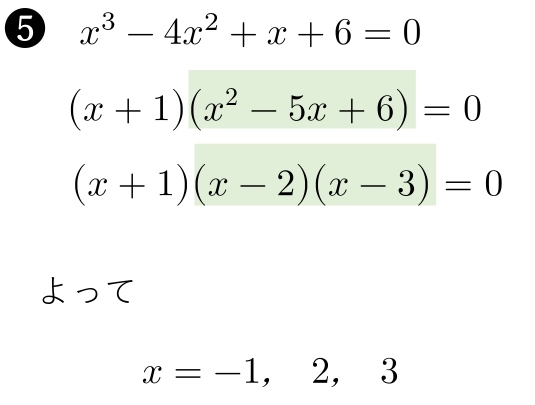
組立除法の余りはいつも \( 0 \) になります。
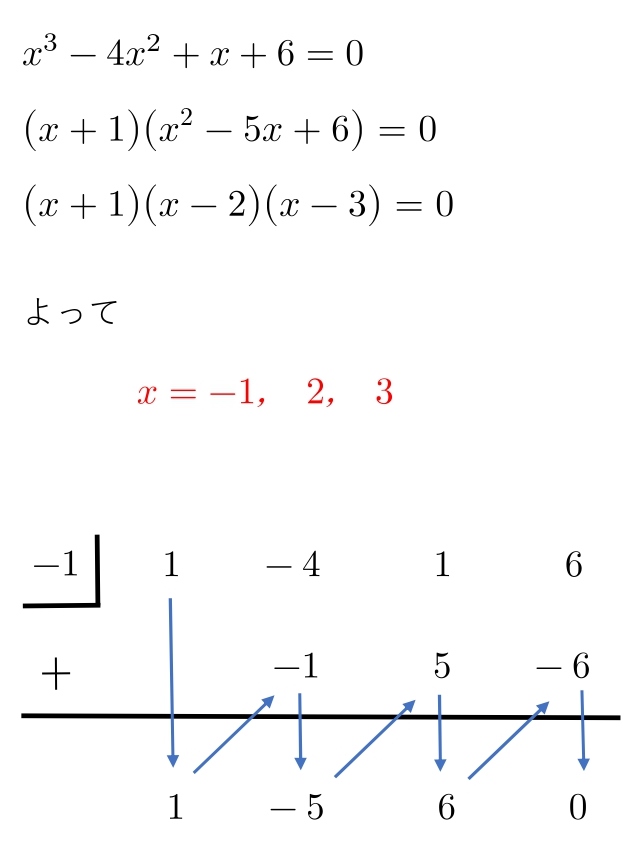
高次方程式の解法を3パターン紹介しましたが、実際は組立除法を使うパターンがほとんどです。
組立除法のやり方はこちらのページで詳しく説明しているので、チェックしてみてください。
このページでは、数学Ⅱの{ ...

【高校数学Ⅱ】組立除法 やり方 詳しい解説(計算方法・公式・問題一覧)
4. 公式まとめ
数学Ⅱ「複素数と方程式」の公式を、PDFファイルでA4プリント1枚にまとめました。
5. 高次方程式の問題
数学Ⅱ「複素数と方程式」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
ぜひチェックしてみてください。
このページでは、数学Ⅱ「Ş ...
【高校数学Ⅱ】複素数と方程式 教科書(問題・解答・公式・解説)

