このページでは、数学Ⅰの「2次関数の平行移動」について解説します。
平行移動の公式と計算方法を,具体的に問題を解きながらわかりやすく解説していきます。公式の丸暗記だけでなく、「なぜ平行移動の公式がマイナスになるのか」理解することが重要です。
問題集を解く際の参考にしてください!

[toc]
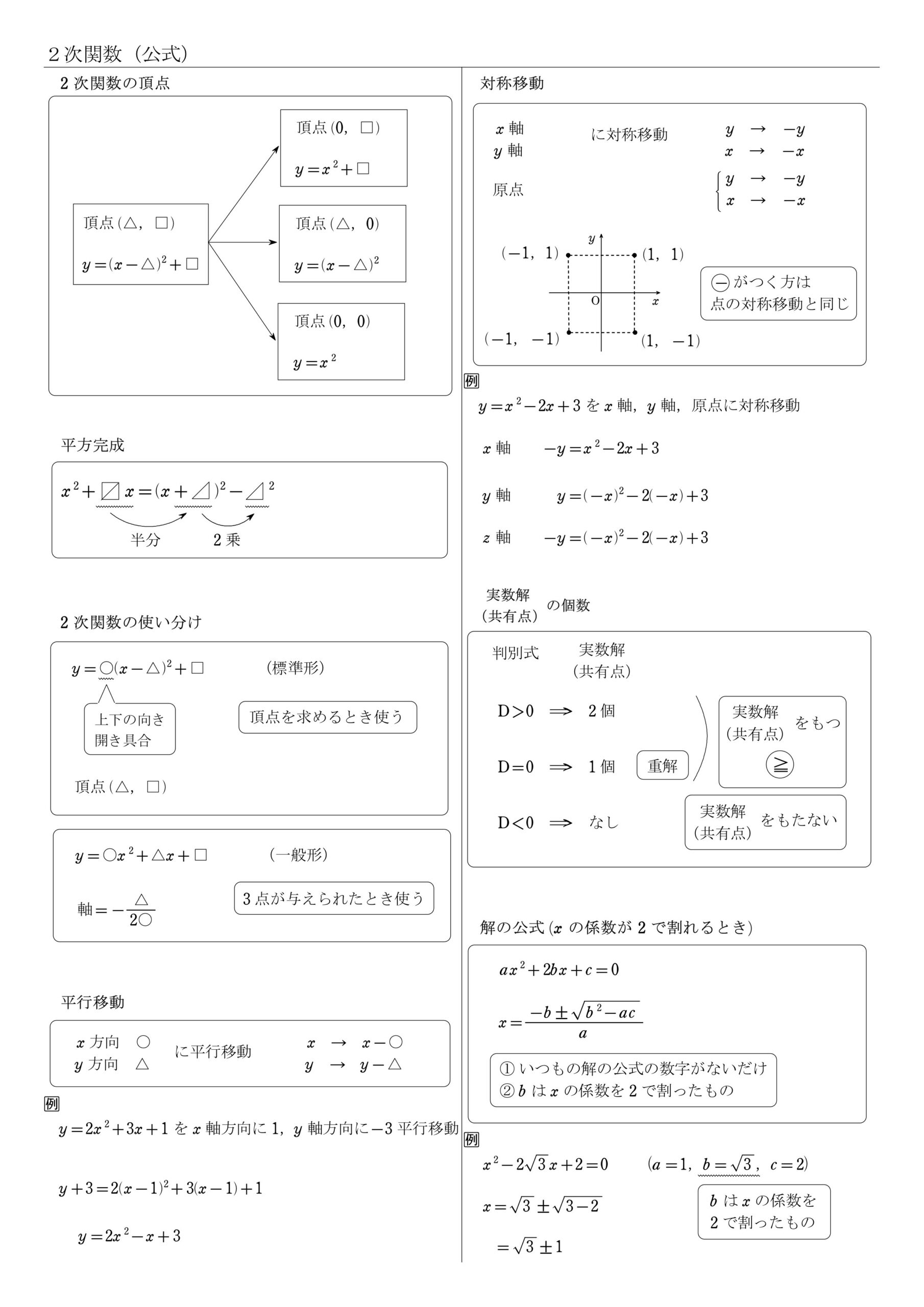
1. グラフの平行移動の公式

2. グラフの平行移動の公式 解説
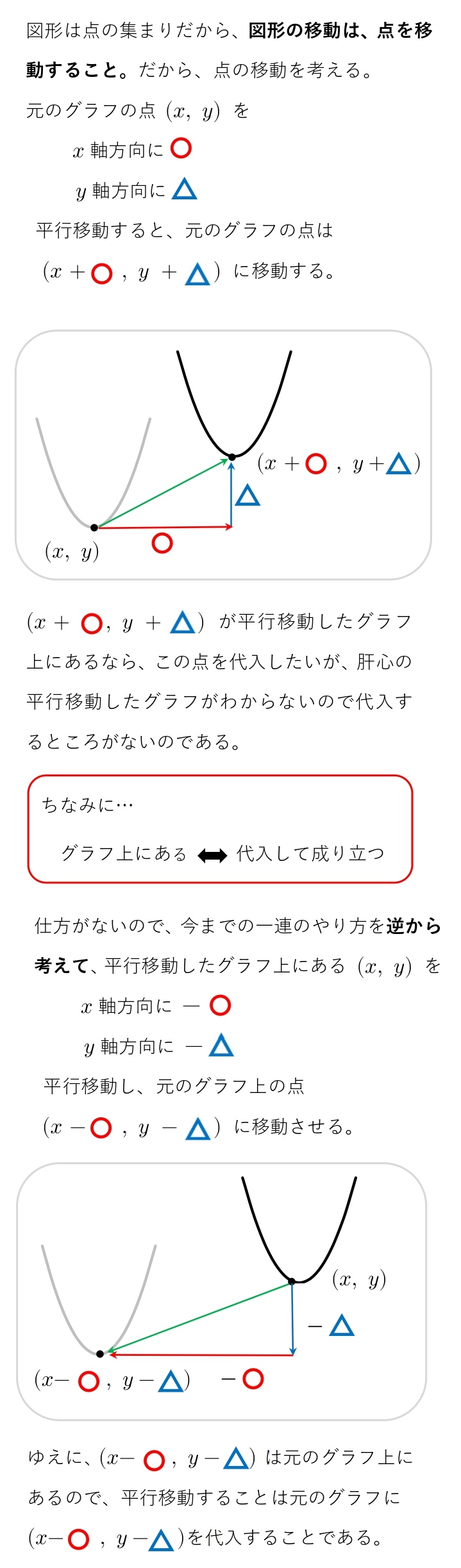
3. グラフの平行移動の問題 解説
\( y=2x^2+5x+3\) のグラフを,\(x\) 軸方向に \(-2\),\(y\) 軸方向に \(1\) だけ平行移動するとき,移動後の放物線の方程式を求めよ。\( \\ \)
\(\hspace{ 15pt }\bbox[#F4E2E2, 2pt, border:]{y}=2\bbox[#DEEBF7, 2pt, border:]{x}^2+5\bbox[#DEEBF7, 2pt, border:]{x}+3\\ \\\)
\(\hspace{ 30pt }\bbox[#DEEBF7, 2pt, border:]{x}\) → \(\bbox[#DEEBF7, 2pt, border:]{x+2}\\ \)
\(\hspace{ 30pt }\bbox[#F4E2E2, 2pt, border:]{y}\) → \(\bbox[#F4E2E2, 2pt, border:]{y-1}\\ \\\)
\(\hspace{ 1pt }\bbox[#F4E2E2, 2pt, border:]{y-1}= 2(\bbox[#DEEBF7, 2pt, border:]{x+2})^2-5(\bbox[#DEEBF7, 2pt, border:]{x+2})+3\\ \\
\hspace{ 5pt }y-1= 2(x^2+4x+4)-5x-10+3\\ \\
\hspace{ 23pt }y= 2x^2+8x+8-5x-6\\ \\
\hspace{ 23pt } \color{#ef5350}{y=2x^2+3x+2} \\ \)
\(x\) に \(x+2\),\(y\) に \(y-1\) を代入するときに \( (\ \ ) \) を忘れずに。
4. 公式まとめ
数学Ⅰ「2次関数」で使う公式をPDF(A4)にまとめました。
5. グラフの平行移動の問題一覧
数学Ⅰ「2次関数」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
ぜひチェックしてみてください。
このページでは、数学Ⅰ「ʌ ...

【高校数学Ⅰ】2次関数 教科書(問題・解答・公式・解説)