このページでは、数学Ⅱの「三角関数のグラフ」をまとめました。
sin・cos・tanのグラフの書き方を、わかりやすく解説していきます。
問題集を解く際の参考にしてください!

[toc]
1. y=sinθ と y=cosθ のグラフ
原点からスタートしたときの \( \sin \) と \( \cos \) のグラフです。
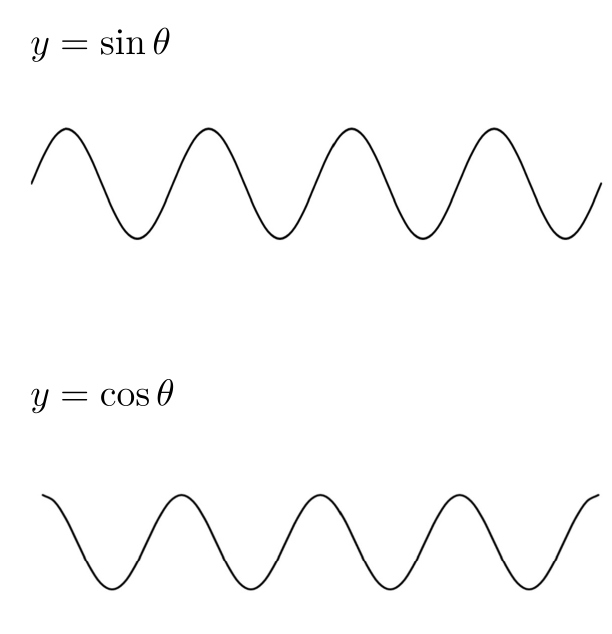
\( \sin \) と \( \cos \) は始まり方が異なるだけで、同じ波線のグラフを描きます。
では、どのように \( \sin \) と \( \cos \) のグラフを区別するでしょうか。
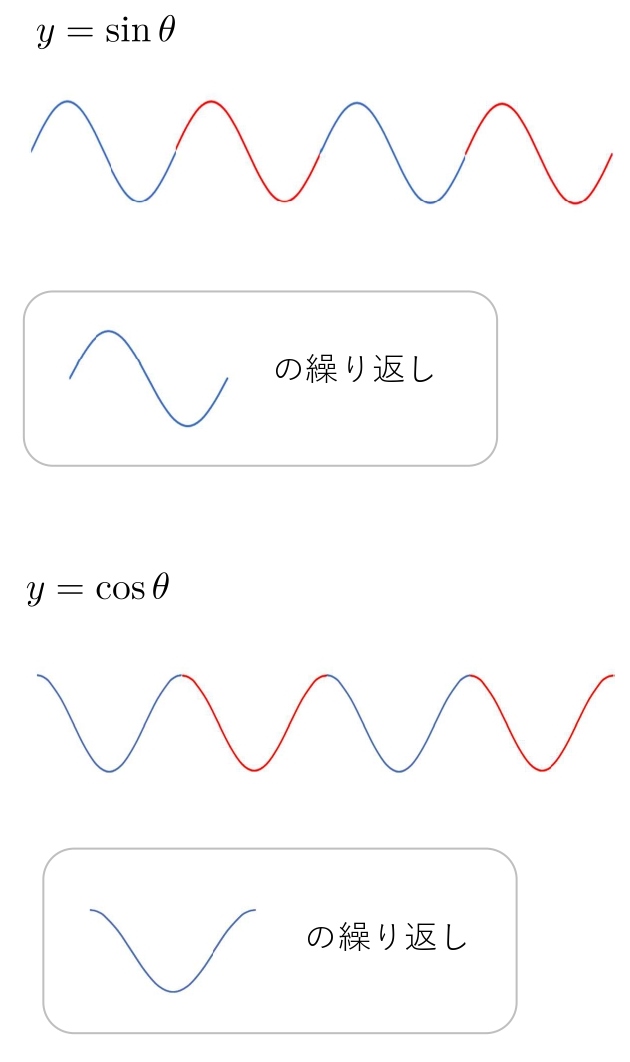
このように \( \sin \) と \( \cos \) は最初の形が異なります。
この最初の形を \( \sin \) と \( \cos \) の基本の形として覚えてください。
最初の形に \( y \) 軸と \( θ \) 軸をつけてみます。
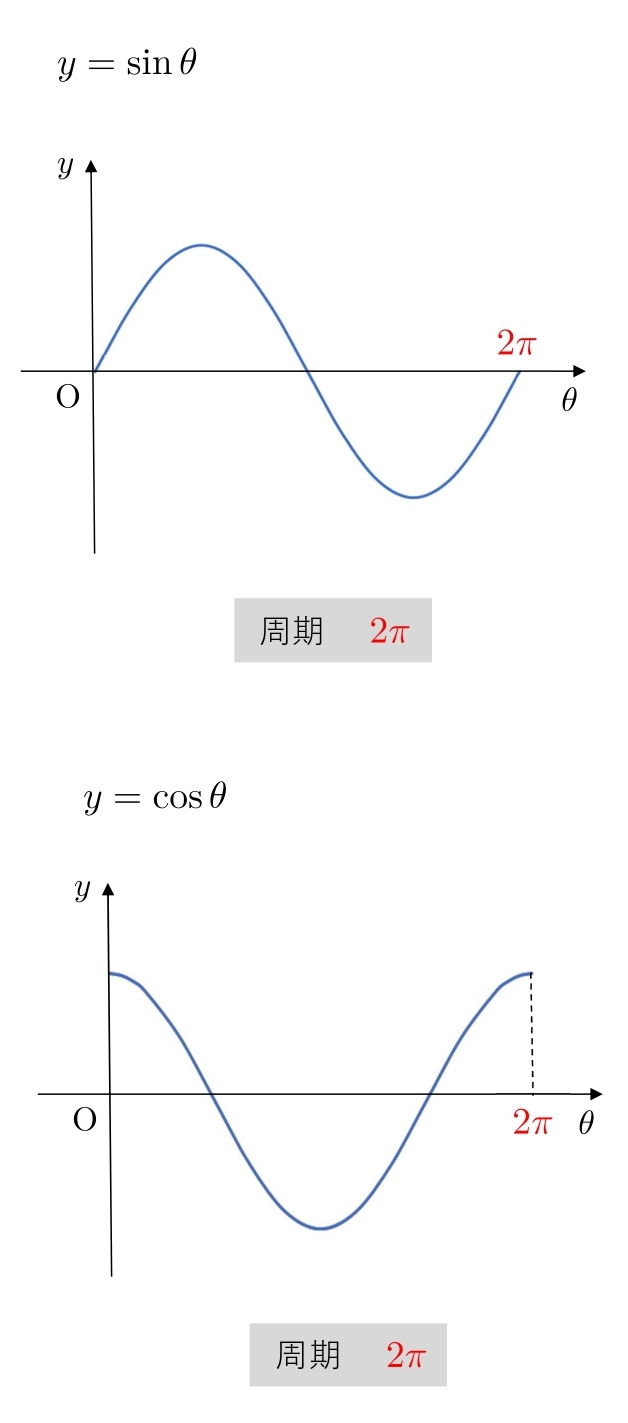
最初の形の繰り返しが現れるまでの \(θ\) の値を、「周期」といいます。
\( \sin \) のグラフは \(0\) から \(2π\) までの形が繰り返すので周期は \(\color{#ef5350}{2π}\)
\( \cos \) のグラフは \(0\) から \(2π\) までの形が繰り返すので周期は \(\color{#ef5350}{2π}\)
となります。
\(θ\) が \(2π\) 以上は繰り返しになるのでグラフを書くときは \(0\) から \(2π\) までとします。
2. y=sinθ のグラフの書き方
まず、\( y \) 軸と \( θ \) 軸を書いて、\( y=\sinθ \) のグラフを書きます。
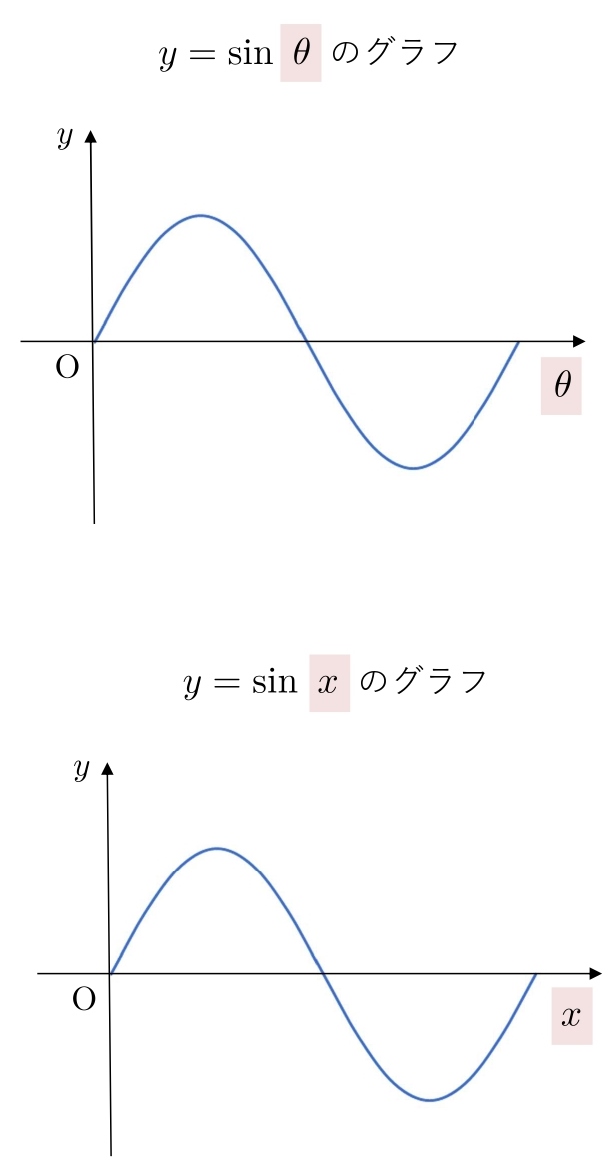
\( y=\sin \bbox[#F4E2E2, 2pt, border:]{θ} \) のとき、\( y \) 軸と \( \bbox[#F4E2E2, 2pt, border:]{θ} \) 軸
\( y=\sin \bbox[#F4E2E2, 2pt, border:]{x} \) のとき、\( y \) 軸と \( \bbox[#F4E2E2, 2pt, border:]{x} \) 軸
となります。
次に、\(0\) と \(2π\) の真ん中に \(\color{#ef5350}{π}\) と書きます。
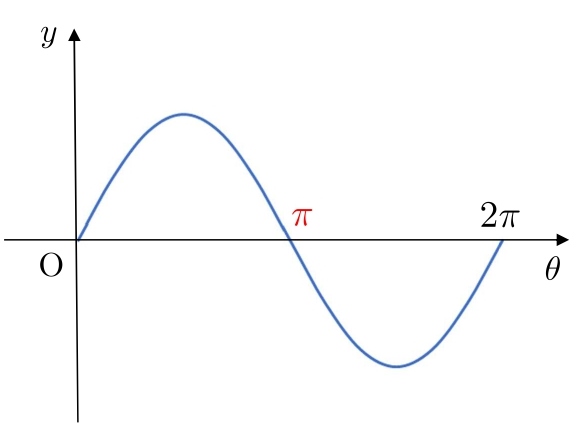
次に、\(0\) と \(π\) の真ん中に \(\displaystyle \color{#ef5350}{\frac{π}{2}}\)
\(π\) と \(2π\) の真ん中に \(\displaystyle \color{#ef5350}{\frac{3}{2}π}\) と書きます。
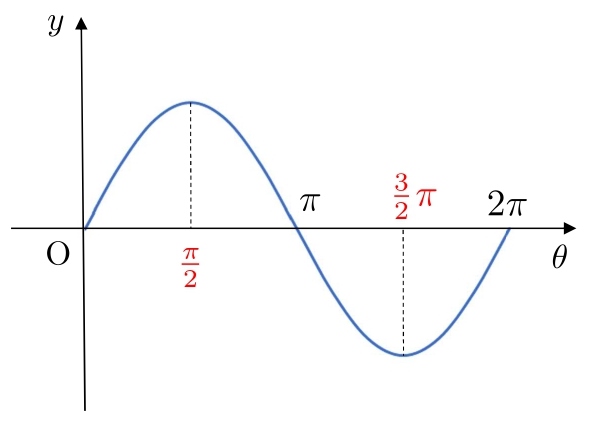
\(π\) と \(2π\) の真ん中は、\(\displaystyle \frac{2}{2}π\) と \(\displaystyle \frac{4}{2}π\) の真ん中なので \(\displaystyle \color{#ef5350}{\frac{3}{2}π}\) です。
最後に、 \( y \) 軸に \( \color{#ef5350}{1} \) と \( \color{#ef5350}{-1} \) を書きます。
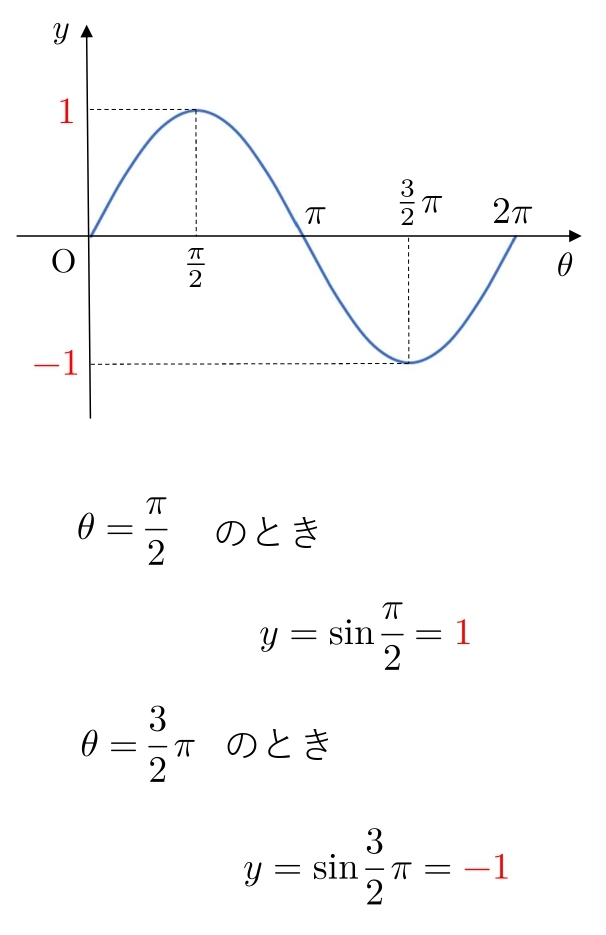
以上が、\( y=\sinθ \) のグラフの書き方です。
sin を拡大・縮小・平行移動したグラフの書き方は、こちらで詳しく説明しているのでぜひチェックしてみてください。
このページでは、数学Ⅱの{ ...

【高校数学Ⅱ】三角関数のグラフ(拡大・縮小・平行移動)
3. y=cosθ のグラフの書き方
\( y=\sinθ \) のグラフと同様に、 \( y \) 軸と \( θ \) 軸をとり、終わりに \(2π\) と書きます。
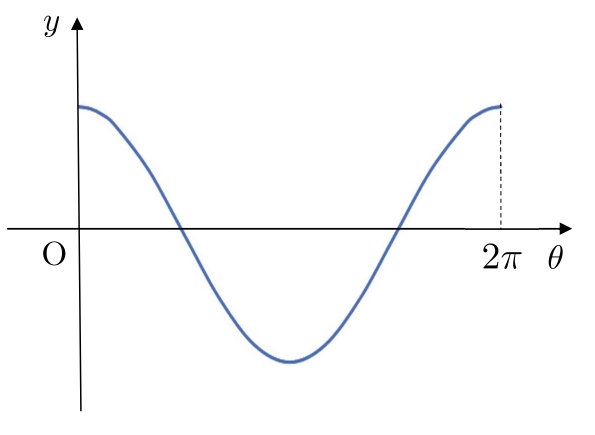
次に、\(0\) と \(2π\) の真ん中に \(\color{#ef5350}{π}\) と書きます。
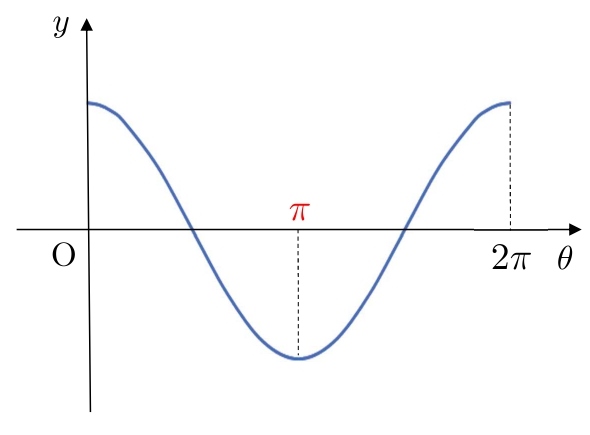
次に、\(0\) と \(π\) の真ん中に \(\displaystyle \color{#ef5350}{\frac{π}{2}}\)
\(π\) と \(2π\) の真ん中に \(\displaystyle \color{#ef5350}{\frac{3}{2}π}\) と書きます。
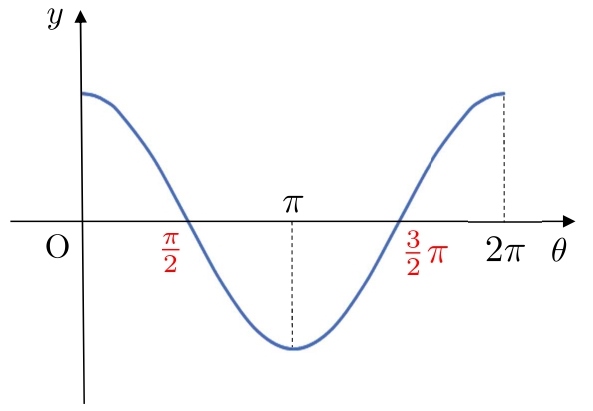
\(π\) と \(2π\) の真ん中は、\(\displaystyle \frac{2}{2}π\) と \(\displaystyle \frac{4}{2}π\) の真ん中なので \(\displaystyle \color{#ef5350}{\frac{3}{2}π}\) です。
最後に、 \( y \) 軸に \( \color{#ef5350}{1} \) と \( \color{#ef5350}{-1} \) を書きます。
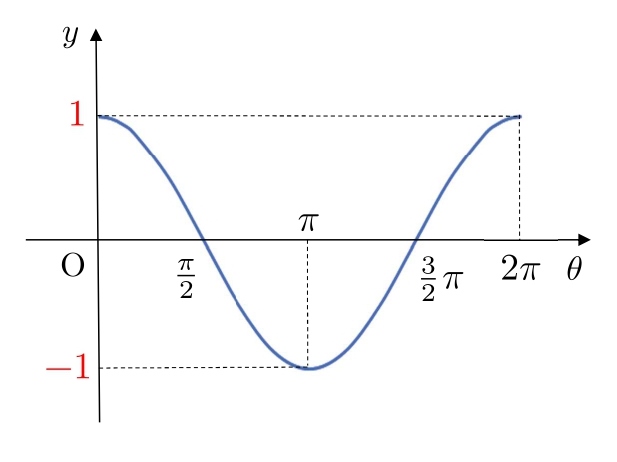
以上が、\( y=\cosθ \) のグラフの書き方です。
4. y=tanθ のグラフの書き方
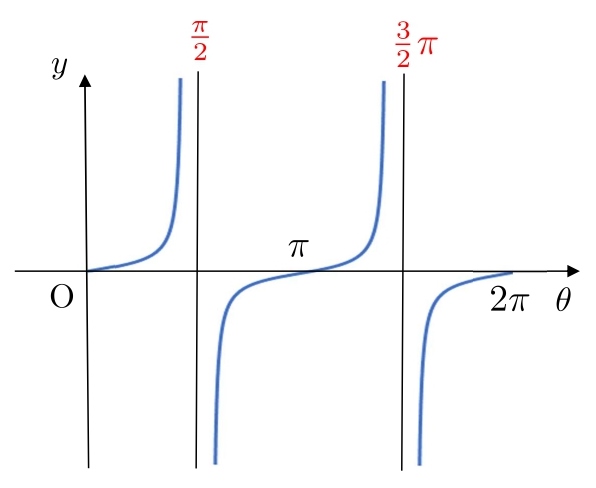
原点からスタートしたときの \( \tan \) のグラフです。
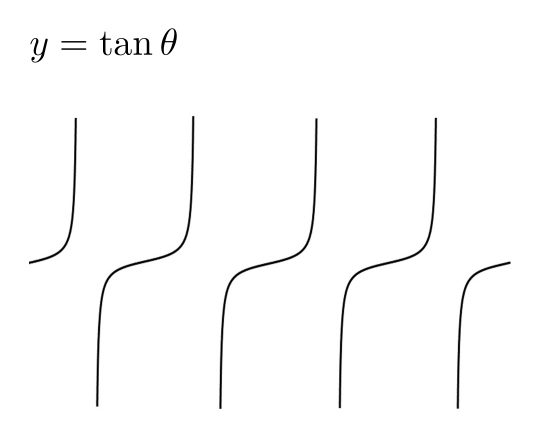
\( \tan \) のグラフは青線が繰り返します。

\( y \) 軸と \( θ \) 軸をつけてみます。
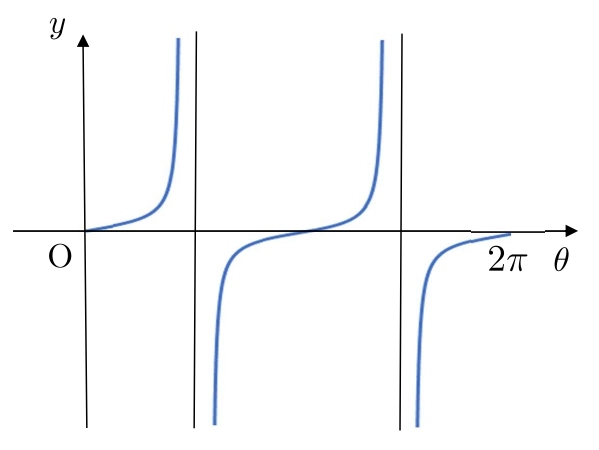
最初の形の繰り返しが現れるまでの \(θ\) の値を、「周期」といいました。
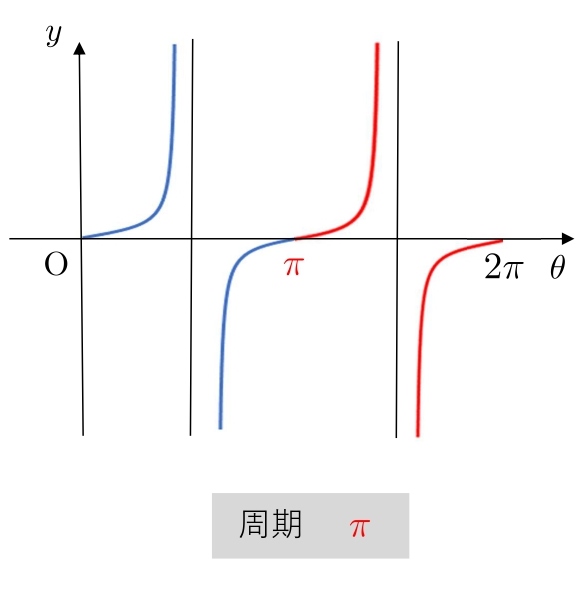
\( \tan \) のグラフは \(0\) から \(π\) までの形が繰り返すので周期は \(\color{#ef5350}{π}\) となります。
周期は \(π\) ですが、\( \sinθ \) と \( \cosθ \) に合わせて \(0\) から \(2π\) までグラフを書きます。
\(0\) と \(2π\) の真ん中に \(\color{#ef5350}{π}\) と書きます。
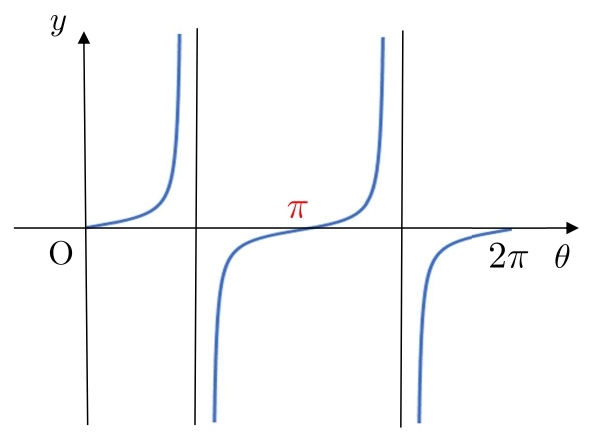
次に、\(0\) と \(π\) の真ん中に \(\displaystyle \color{#ef5350}{\frac{π}{2}}\)
\(π\) と \(2π\) の真ん中に \(\displaystyle \color{#ef5350}{\frac{3}{2}π}\) と書きます。
\(π\) と \(2π\) の真ん中は、\(\displaystyle \frac{2}{2}π\) と \(\displaystyle \frac{4}{2}π\) の真ん中なので \(\displaystyle \color{#ef5350}{\frac{3}{2}π}\) です。
縦線は「漸近線」といいます。
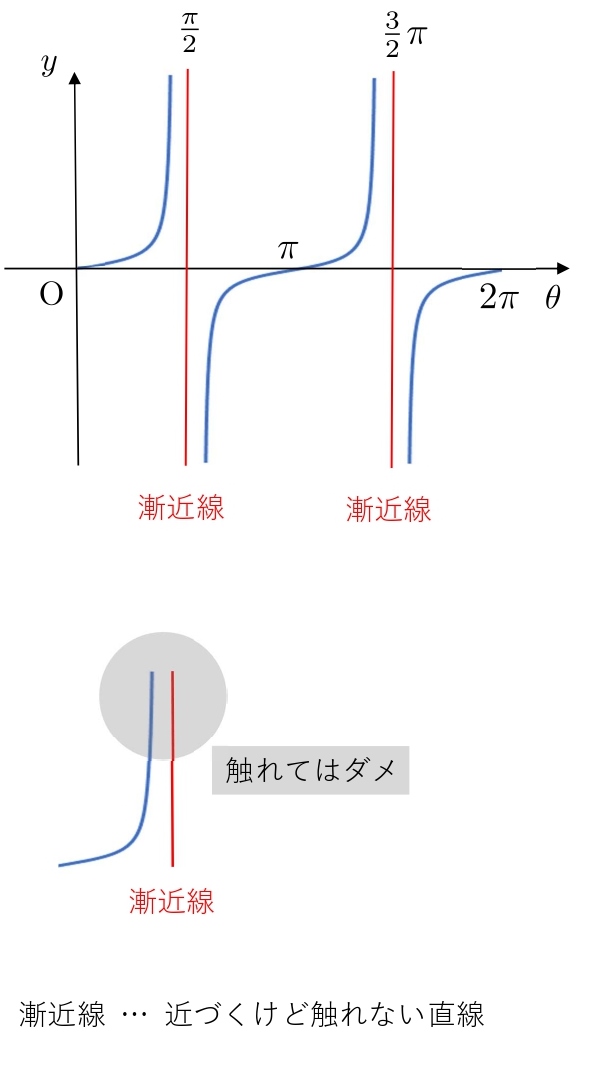
「漸近線」は触れてはいけないので、グラフを書くときは触れないように注意してください。
以上が、\( y=\tanθ \) のグラフの書き方です。
拡大・縮小・平行移動したグラフの書き方は、こちらで詳しく説明しているのでぜひチェックしてみてください。
このページでは、数学Ⅱの{ ...

【高校数学Ⅱ】三角関数のグラフ(拡大・縮小・平行移動)
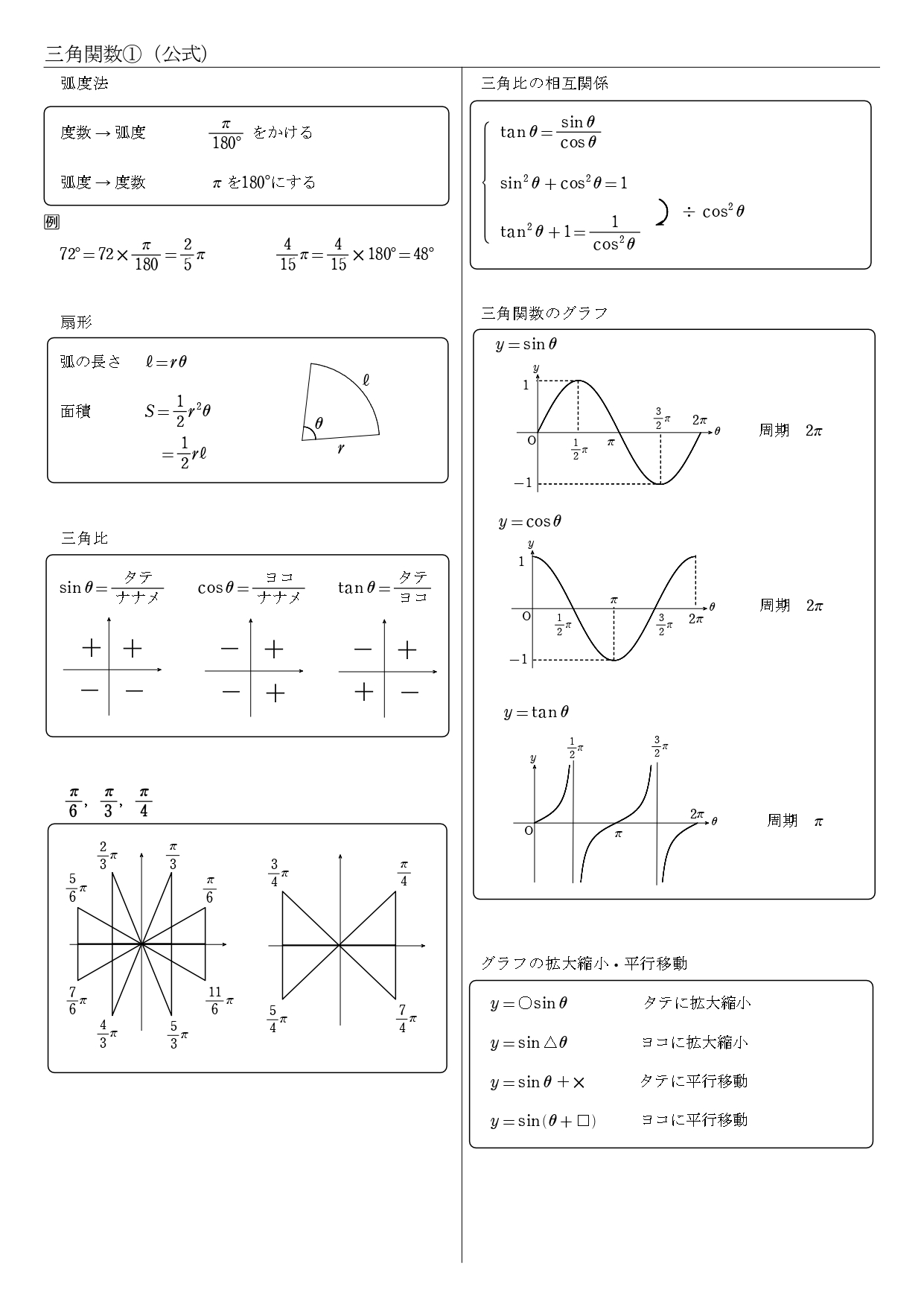
5. 公式まとめ
数学Ⅱ「三角関数」の公式一覧を、PDFファイルでA4プリント1枚にまとめました。
6. 三角関数の問題
数学Ⅱ「三角関数」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
ぜひチェックしてみてください。
このページでは、数学Ⅱ「Ç ...

【高校数学Ⅱ】三角関数 教科書(問題・解答・公式・解説)