このページでは、数学Ⅱの「三角関数のグラフ」をまとめました。
sin cos tan を拡大縮小・平行移動したグラフの書き方を、わかりやすく解説していきます。
問題集を解く際の参考にしてください！
sin cos tan のグラフの書き方はこちらで詳しく説明しているのでぜひチェックしてみてください。
1. グラフの種類
数字のある場所で見分けます。
まずは、どのパターンのグラフなのか覚えましょう。
拡大縮小・平行移動したグラフの書き方は、sin と cos 同じなので、sinを例にして説明していきます。
2. y=●sinθ のグラフ
\( y=●\sinθ \) はタテの拡大縮小を表しています。
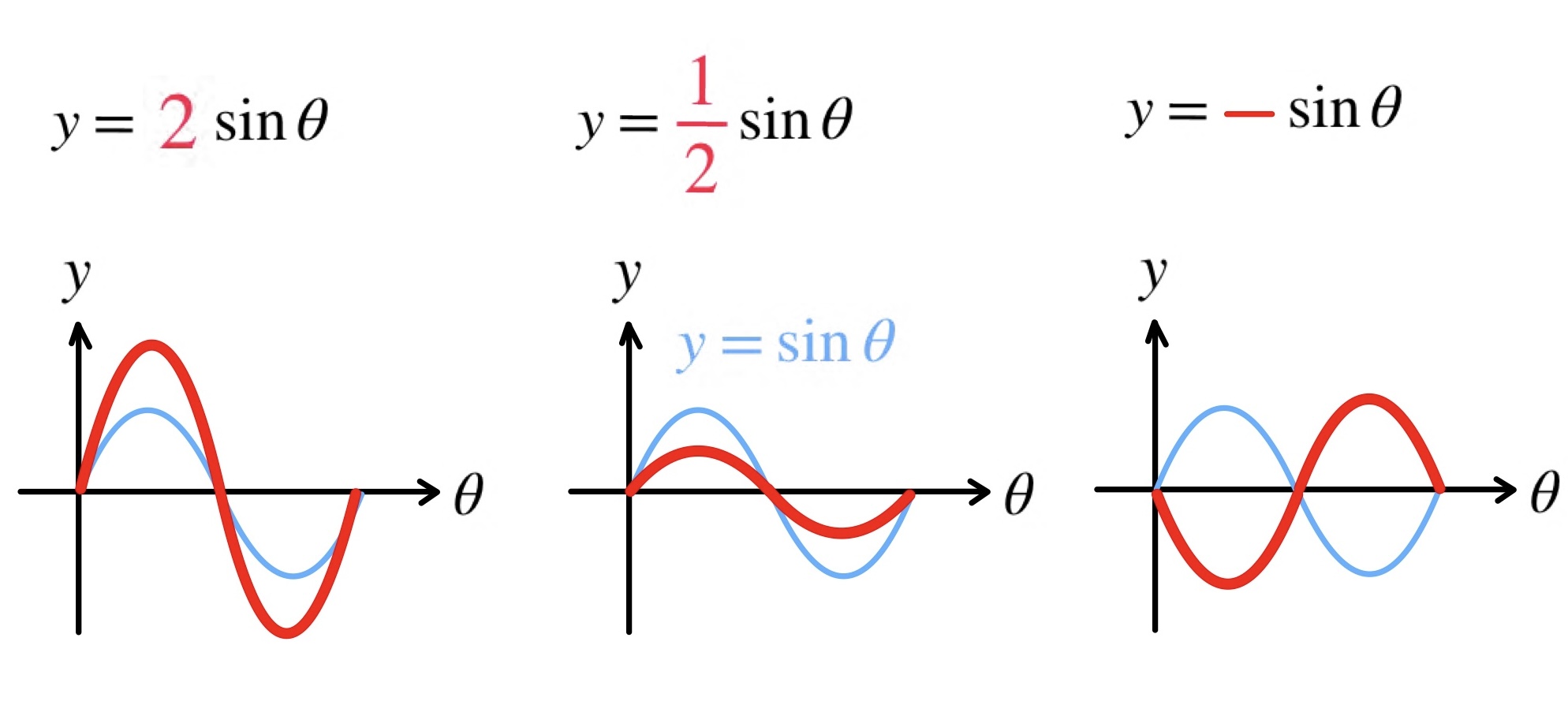
実際に、問題を解いていきます。
次の関数のグラフを書け。
(1) \( y=2\sinθ \)
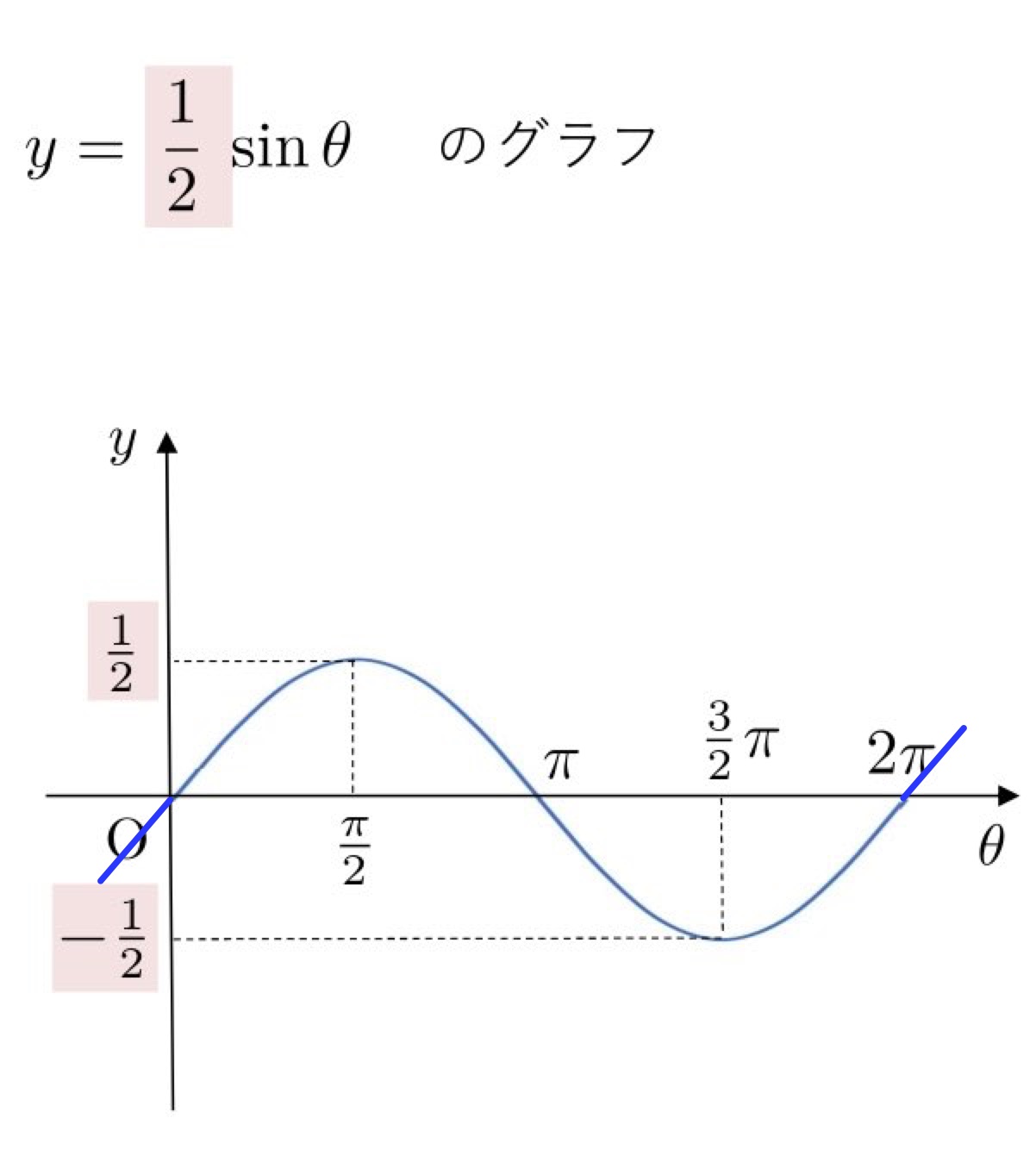
(2) \( y=\displaystyle{\frac{1}{2}}\sinθ \)
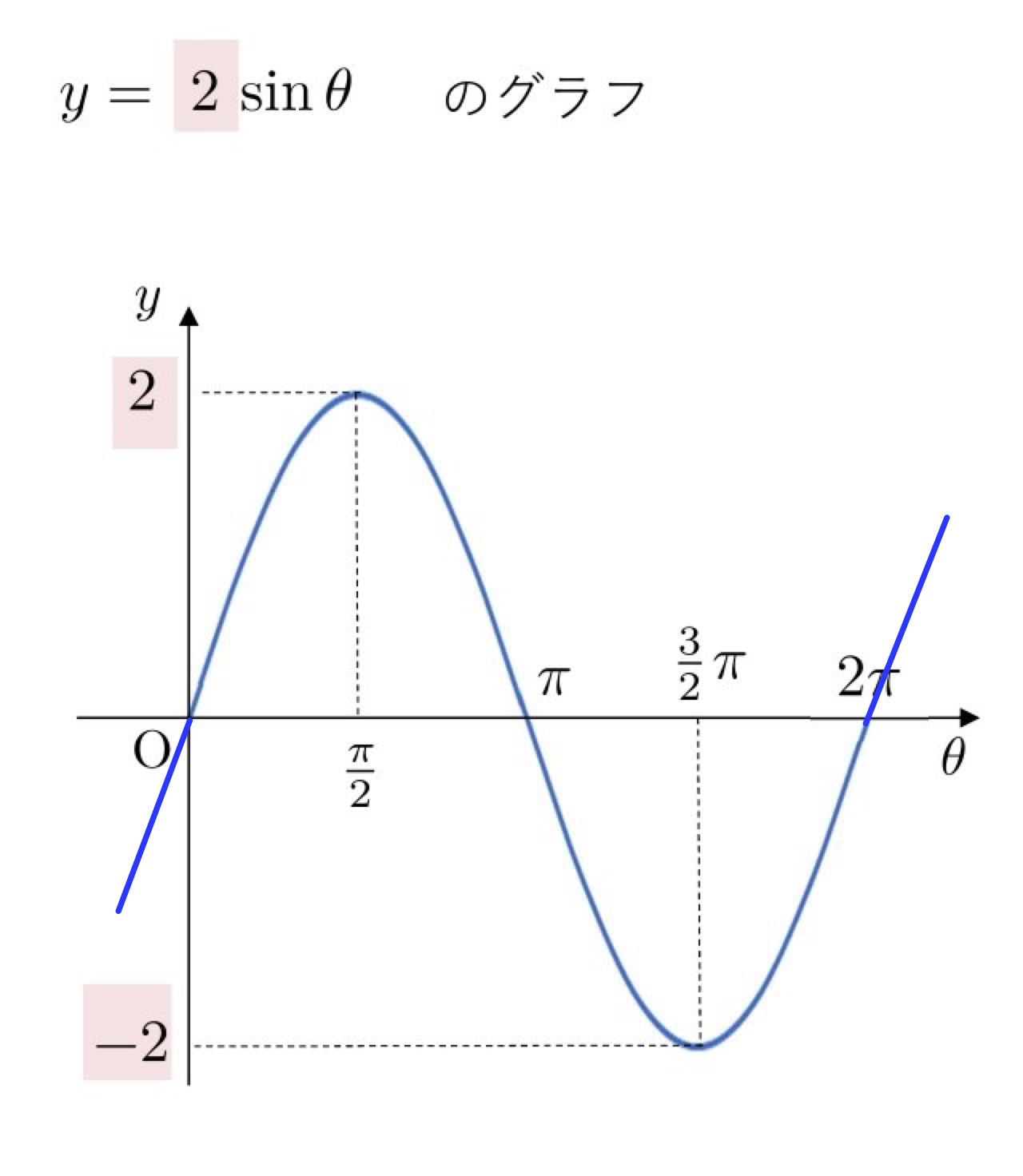
\( y=\bbox[#F4E2E2, 2pt, border:]{2}\sinθ \) は、タテが \(\bbox[#F4E2E2, 2pt, border:]{2}\) 倍になります。
\( y=\displaystyle\bbox[#F4E2E2, 2pt, border:]{\frac{1}{2}}\sinθ \) は、タテが \(\displaystyle\bbox[#F4E2E2, 2pt, border:]{\frac{1}{2}}\) 倍になります。
3. y=sin▲θ のグラフ
\( y=\sin▲θ \) はヨコの拡大縮小を表しています。
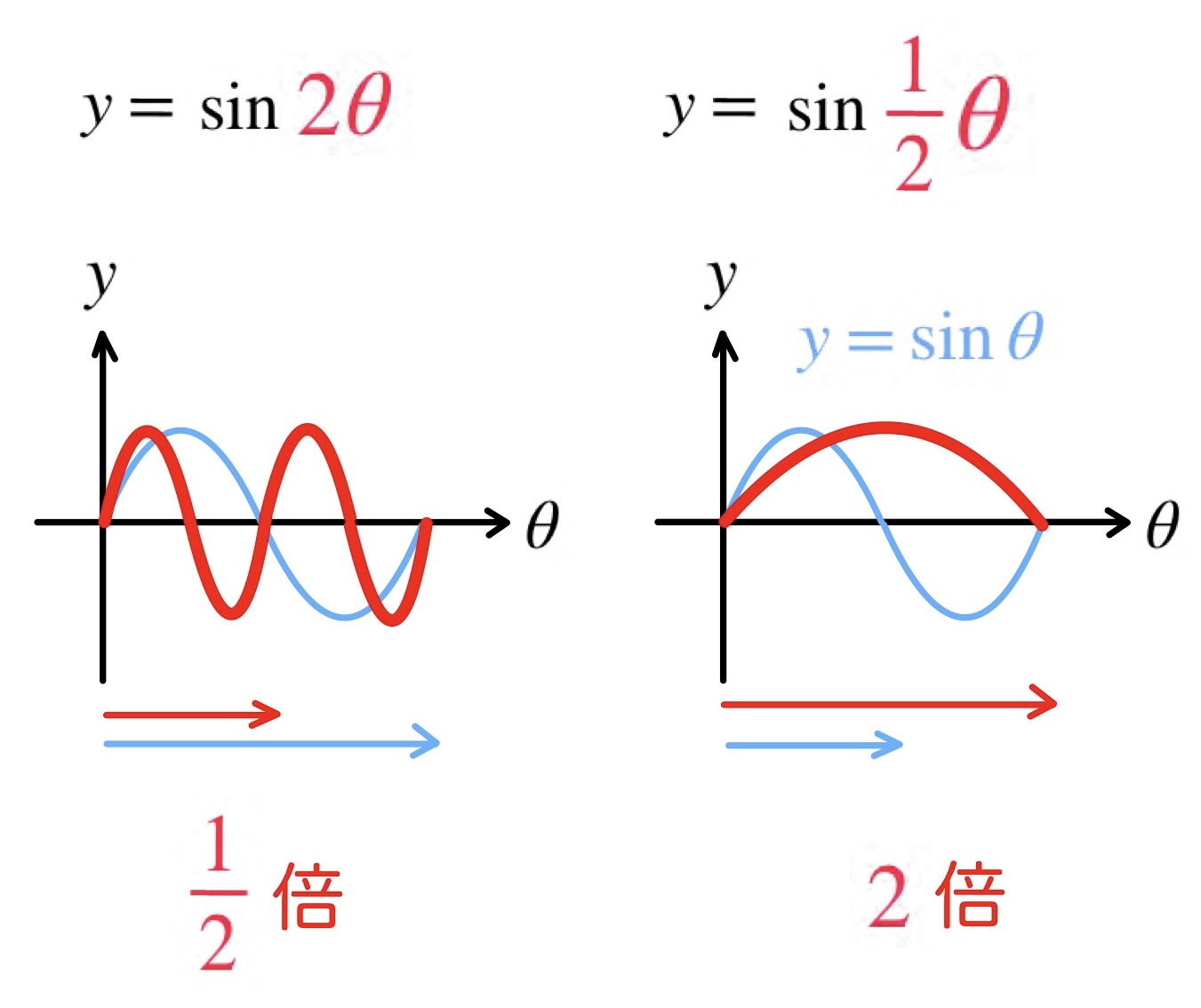
実際に、問題を解いていきます。
次の関数のグラフを書け。
(1) \( y=\sin2θ \)
(2) \( y=\sin\displaystyle{\frac{3}{2}}θ \)
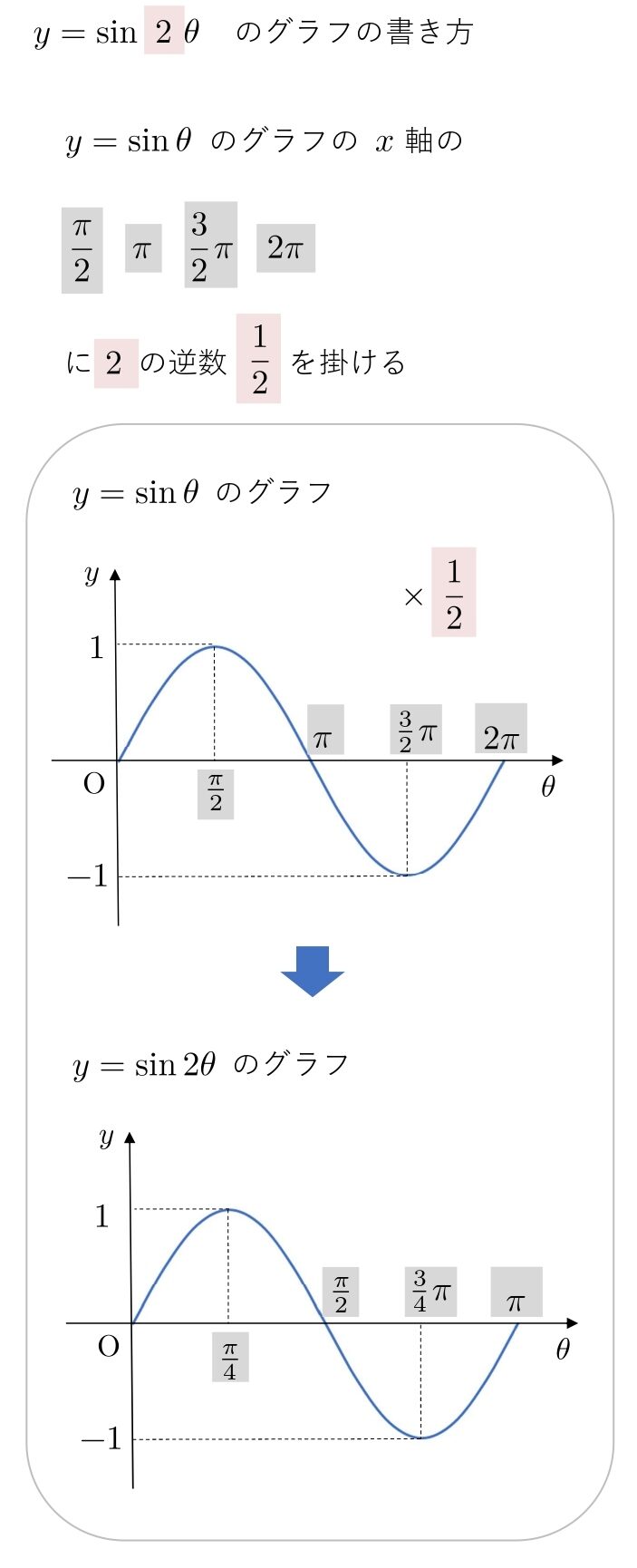
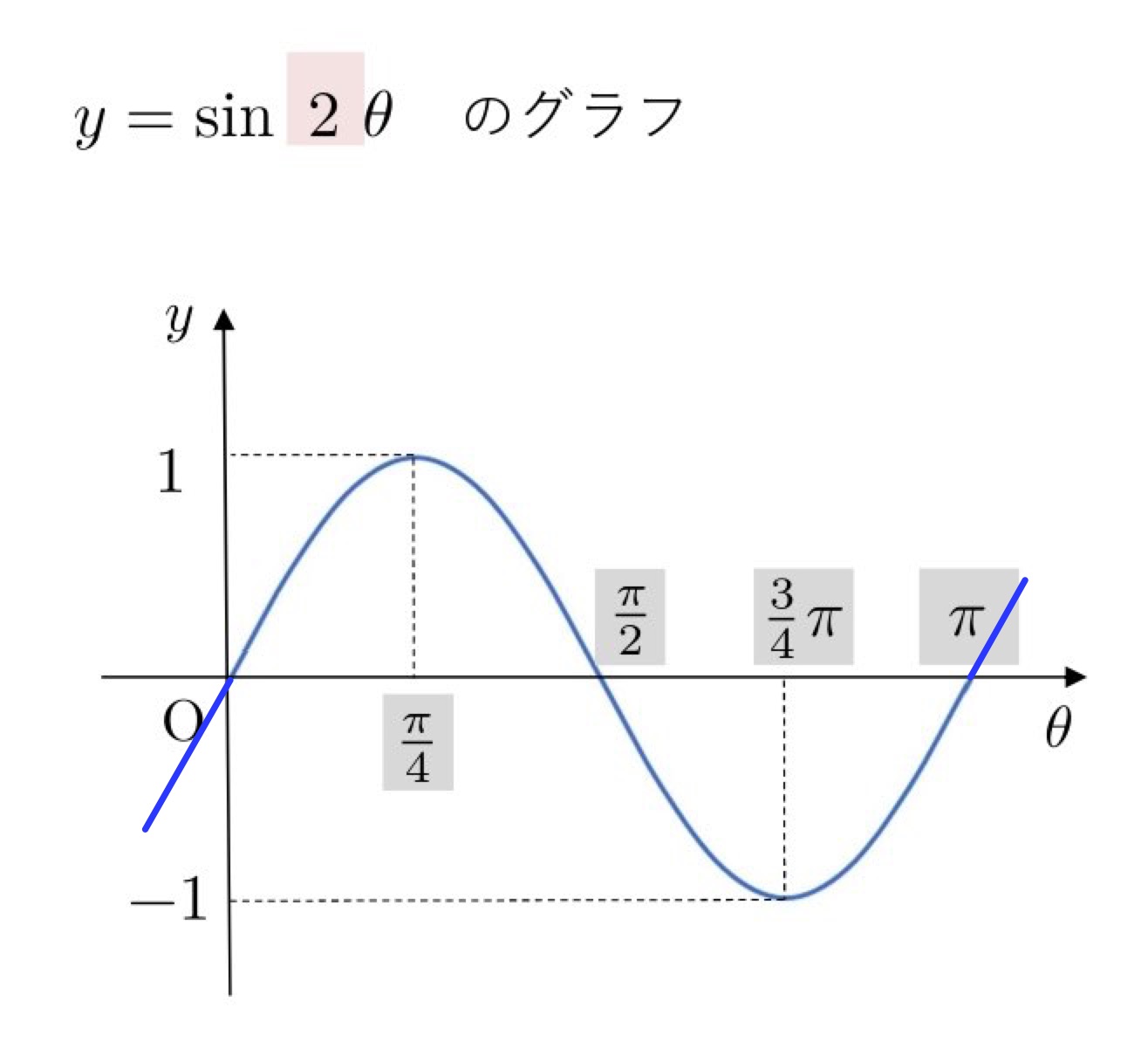
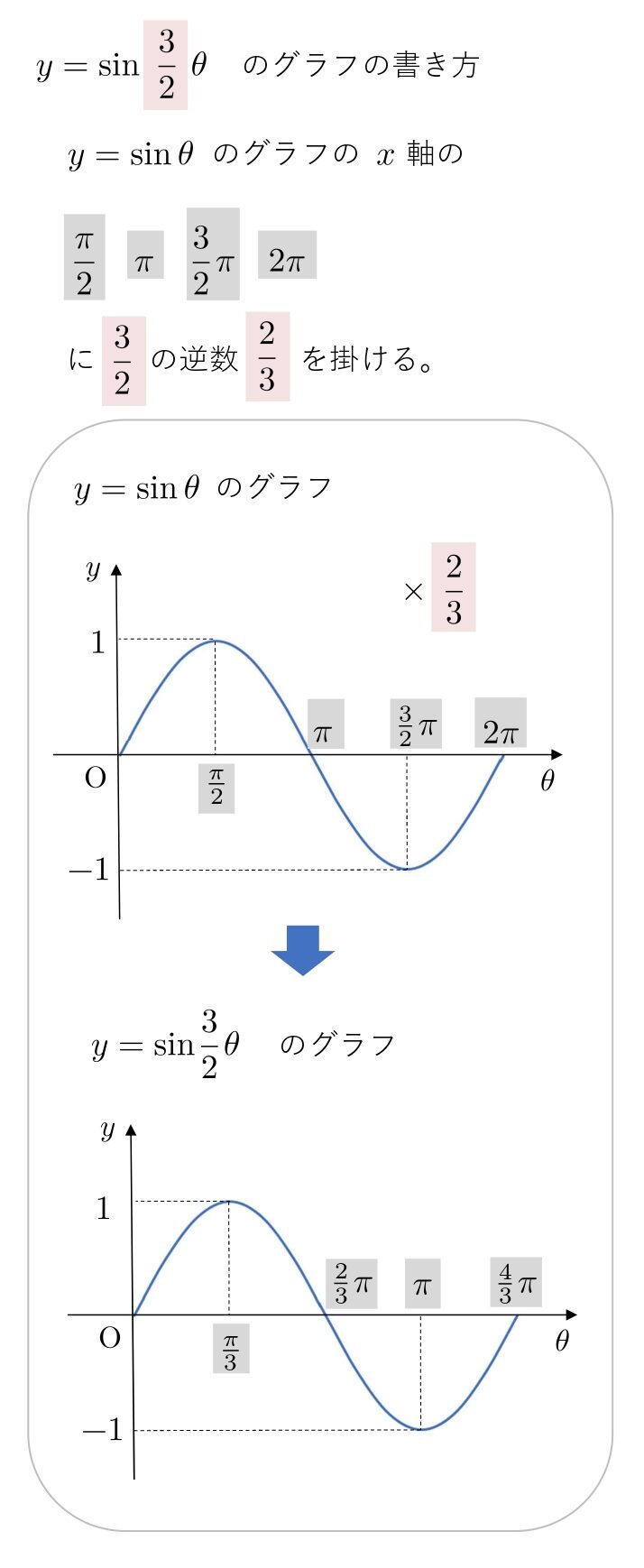
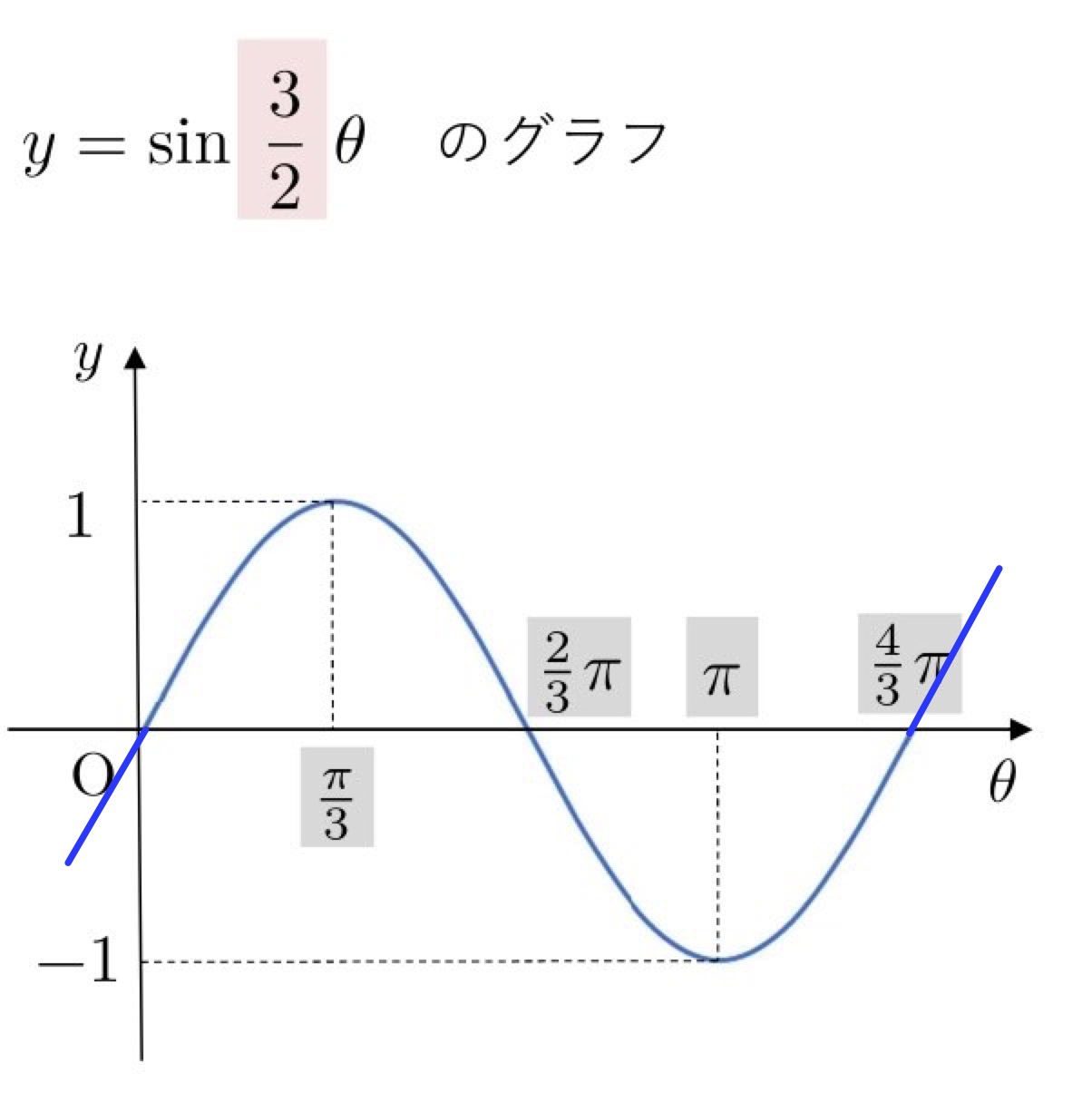
逆数をかけるので注意してください。
4. y=sinθ+✕ のグラフ
\( y=\sinθ＋✖ \) はタテの平行移動を表しています。
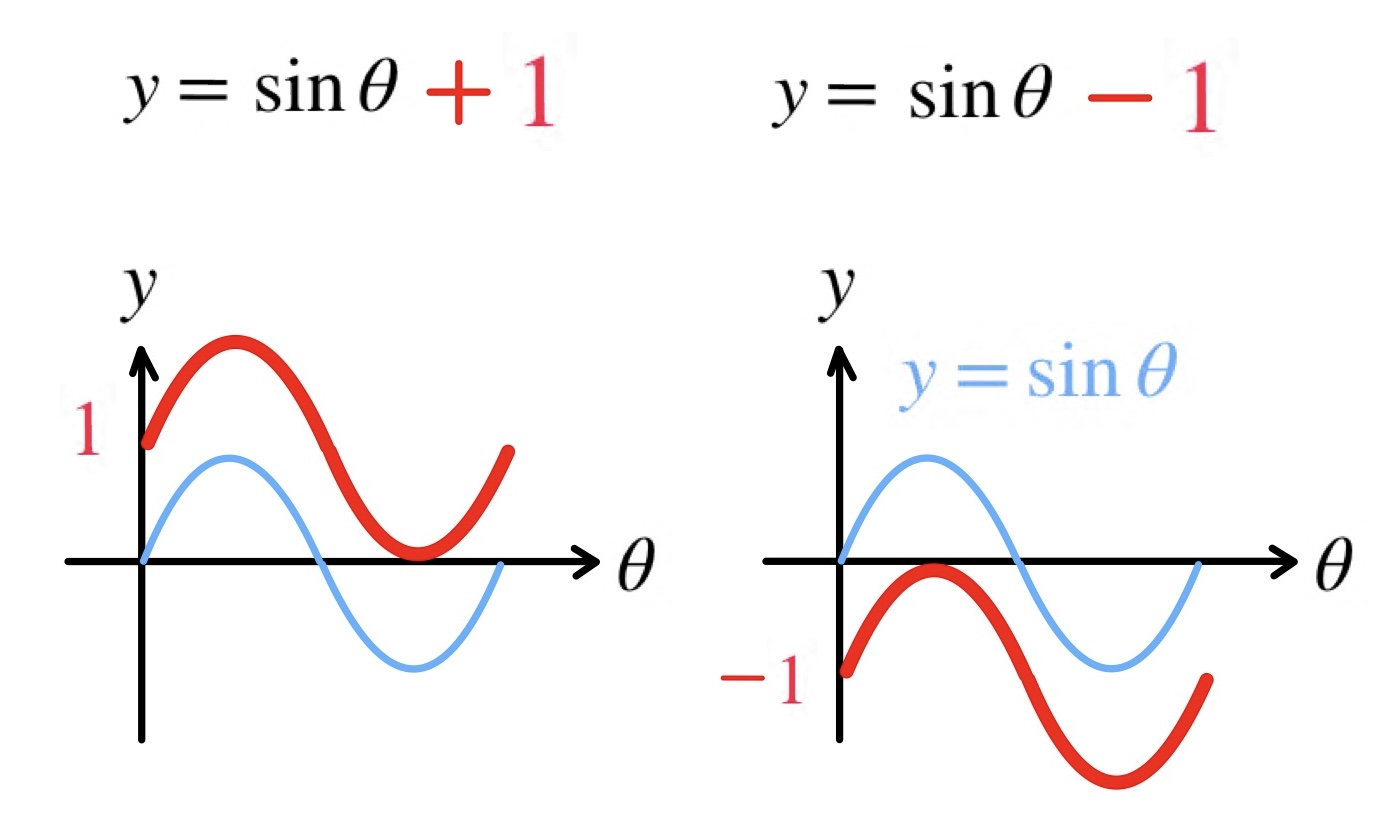
実際に、問題を解いていきます。
次の関数のグラフを書け。
(1) \( y=\sinθ+1 \)
(2) \( y=\sinθ-1 \)
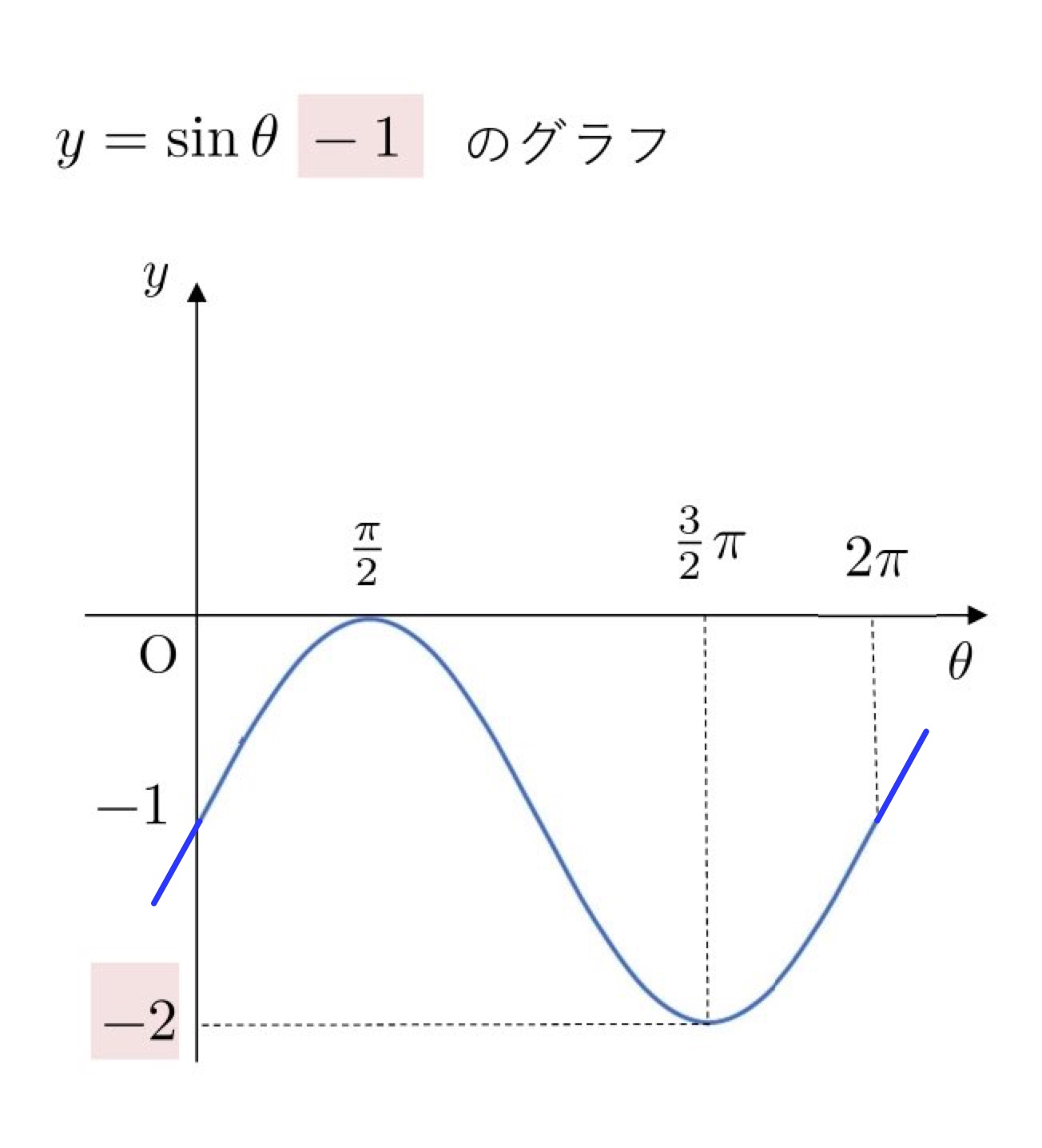
5. y=sin(θ-■) のグラフ
\( y=\sin(θ-■) \) はヨコの平行移動を表しています。
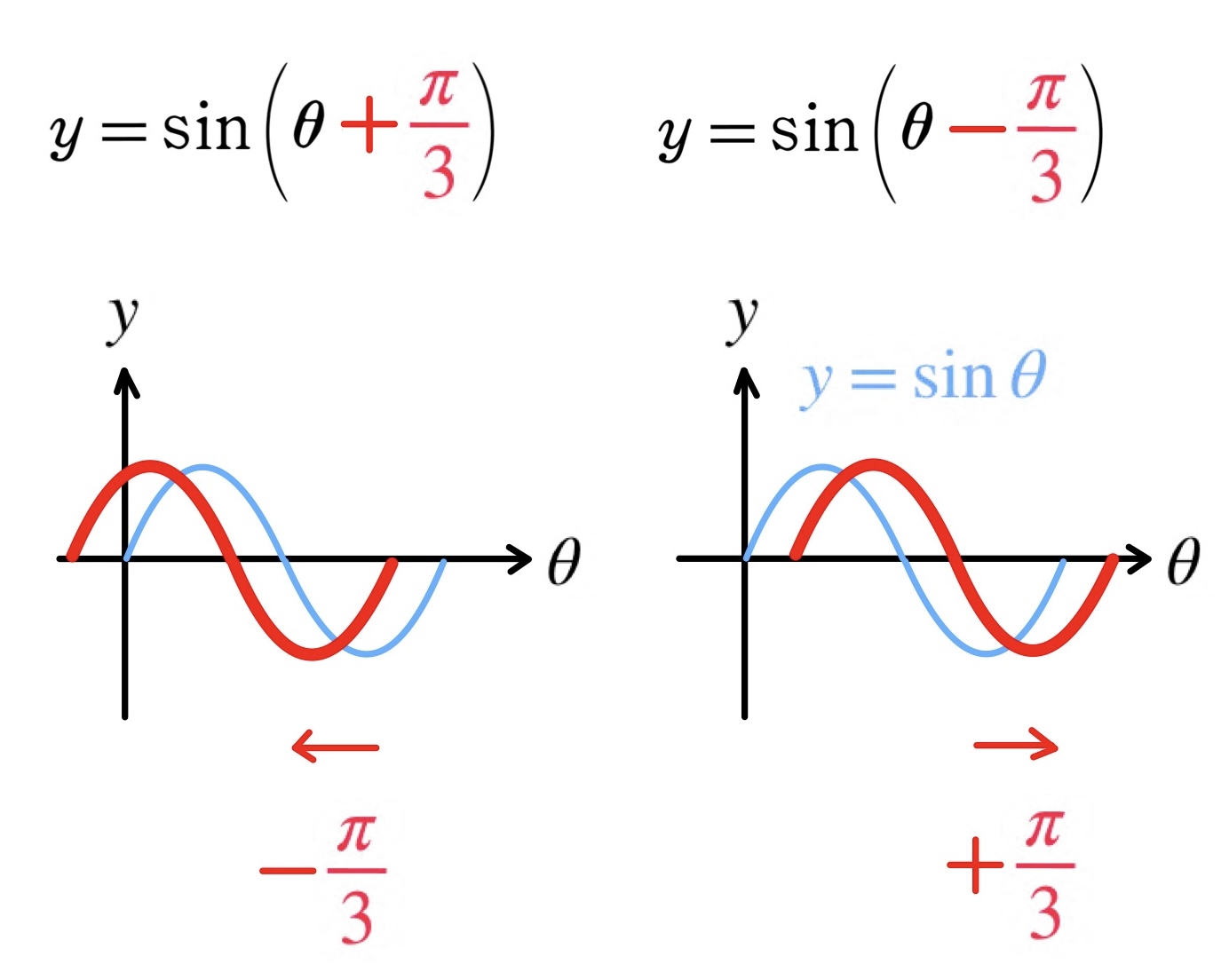
実際に、問題を解いていきます。
次の関数のグラフを書け。
\( y=\sin\left(θ+\displaystyle{\frac{π}{6}}\right) \)
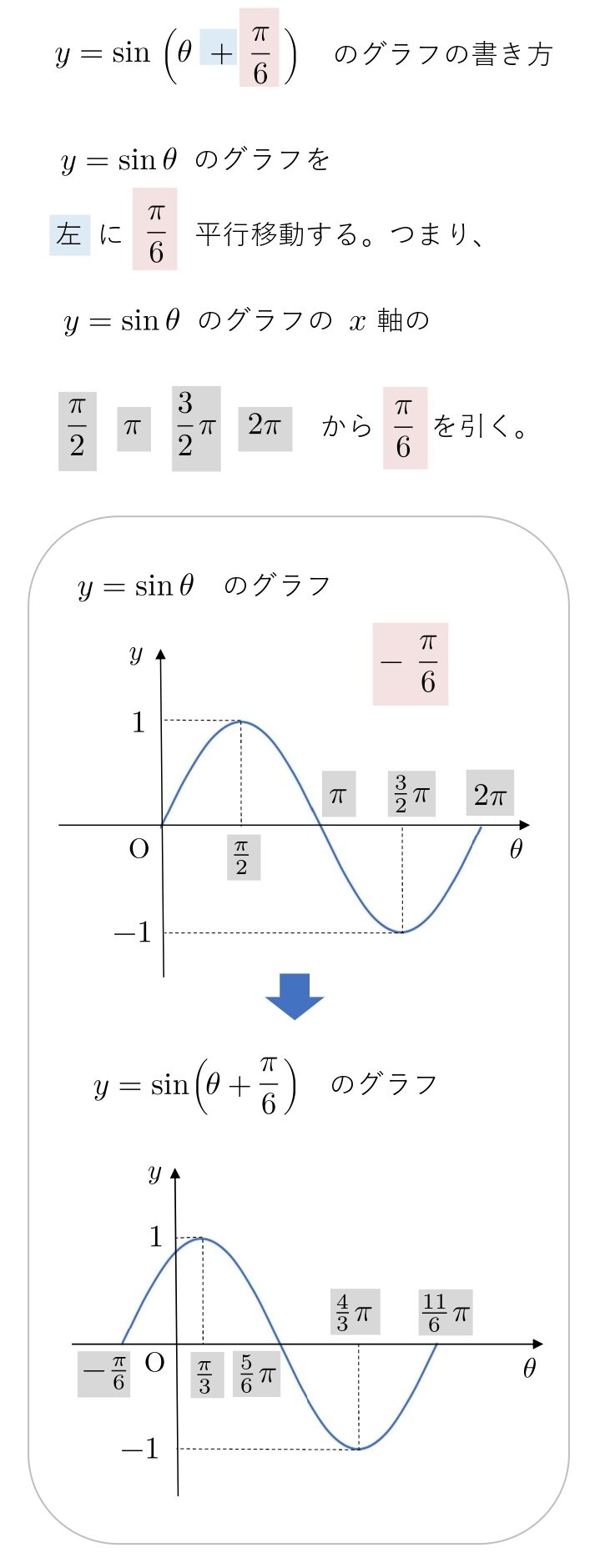
\(\displaystyle y=\sin \left(θ \bbox[#DEEBF7, 2pt, border:]{+}\bbox[#F4E2E2, 2pt, border:]{\frac{π}{6}}\right) \) は、左に \( \displaystyle \bbox[#F4E2E2, 2pt, border:]{\frac{π}{6}}\) 平行移動します。
もし、\(\displaystyle y=\sin \left(θ \bbox[#DEEBF7, 2pt, border:]{-}\bbox[#F4E2E2, 2pt, border:]{\frac{π}{6}}\right) \) だったら、右に \( \displaystyle \bbox[#F4E2E2, 2pt, border:]{\frac{π}{6}}\) 平行移動します。
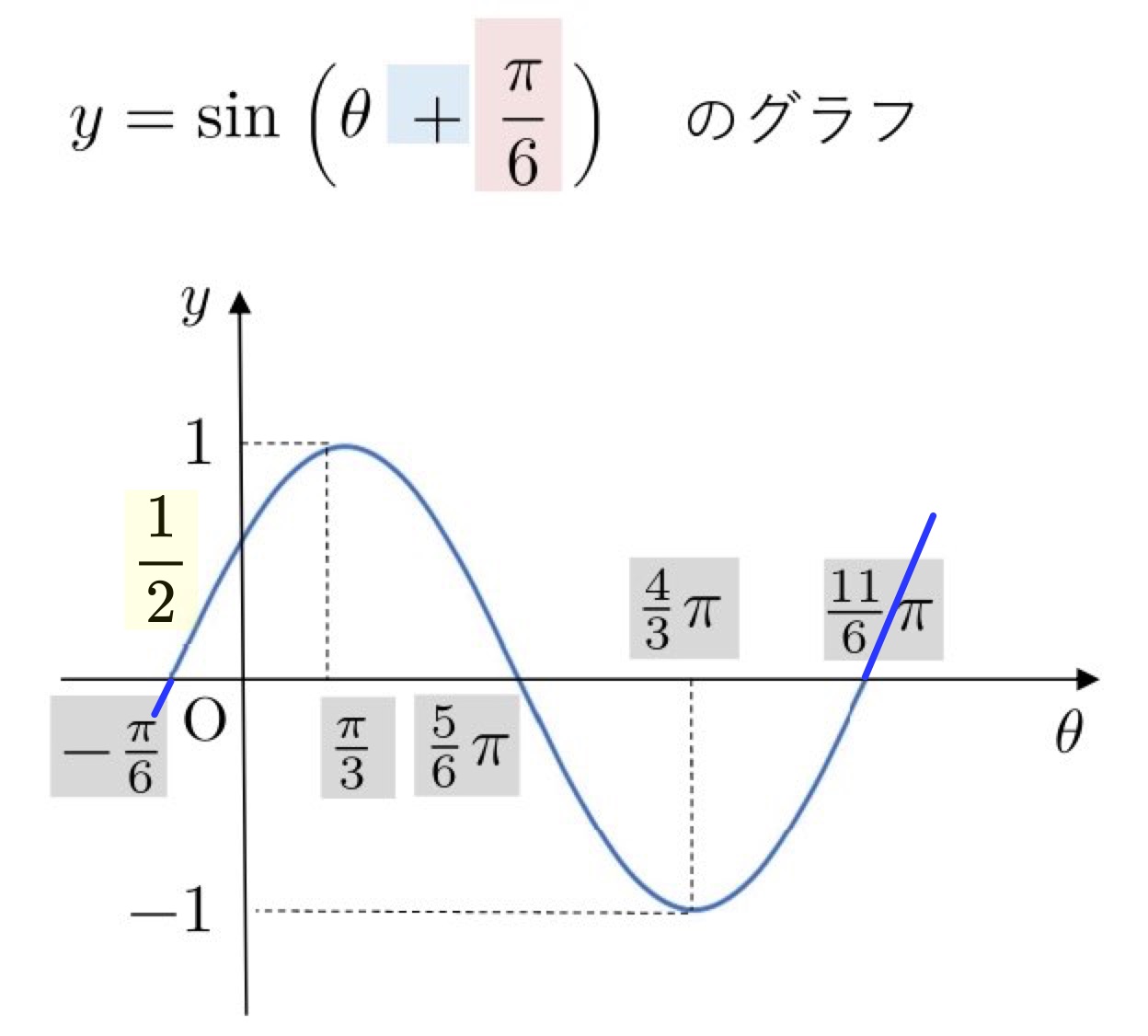
\(y\) 軸との交点は、\( y=\sin\left(θ+\displaystyle{\frac{π}{6}}\right) \) の \(θ\) に \(0\) を代入します。
そうすると、\(\displaystyle y=\sin\frac{π}{6}=\frac{1}{2} \) になります。
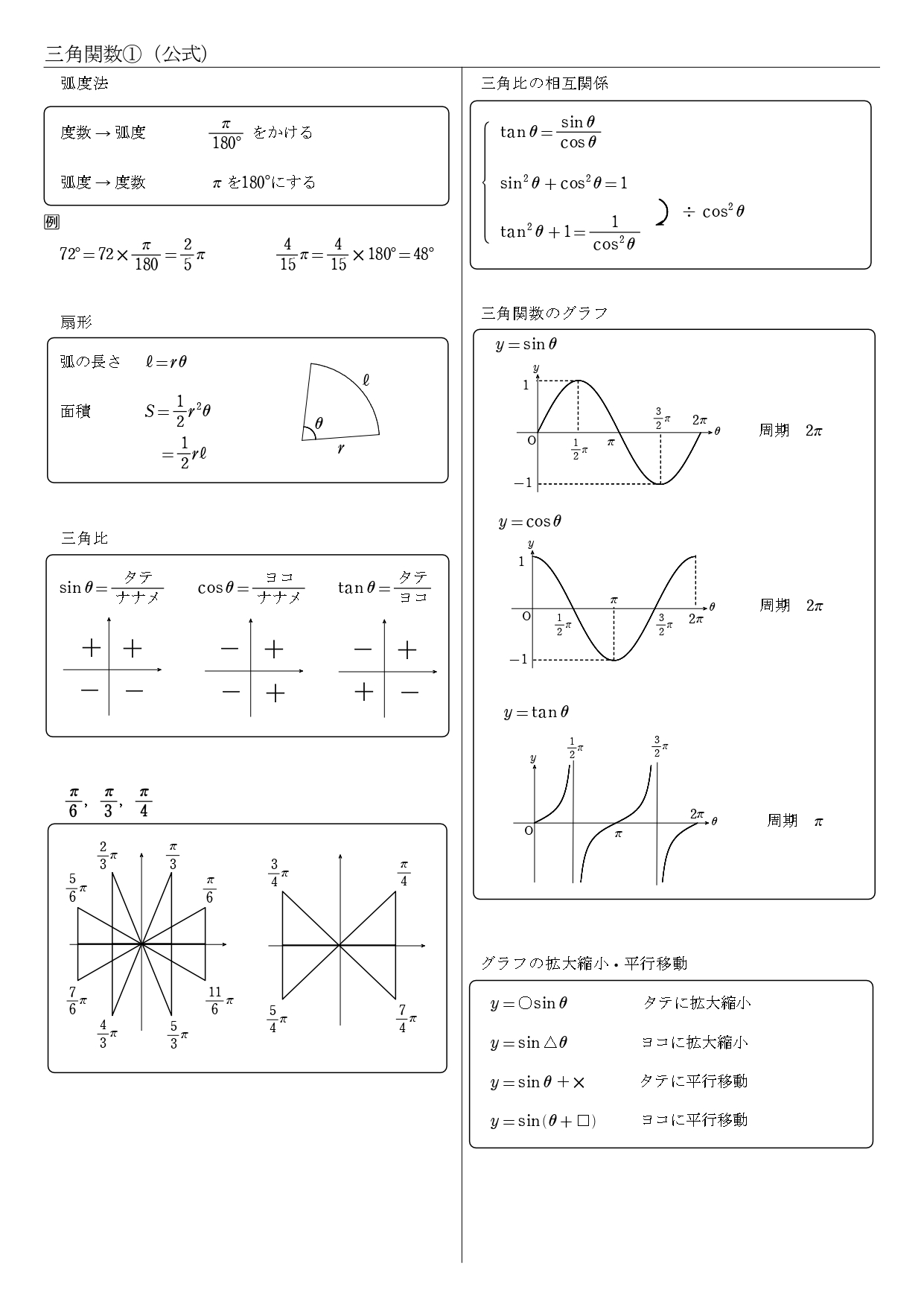
6. 公式まとめ
数学Ⅱ「三角関数」の公式一覧を、PDFファイルでA4プリント１枚にまとめました。
7. 三角関数の問題一覧
数学Ⅱ「三角関数」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
