このページでは、数学Ⅱ「微分法」の導関数の定義をまとめました。
導関数の定義の覚え方、問題をわかりやすく解説していきます。
問題集を解く際の参考にしてください！
1. 導関数とは
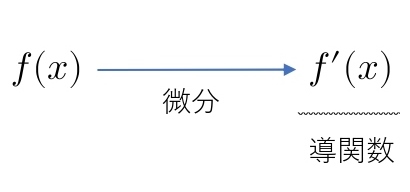
\( f(x) \) を微分したものを導関数といいます。
たとえば…
\( f(x)=2x^2+3 \)
導関数は \( f(x) \) を微分したものなので
\( f'(x)=4x \)
となります。
導関数は \( f'(x)=4x \) のように関数（文字の入った式）になります。
ただし、\( f(x) \) が１次式の場合は値になります。
\( f(x)=2x \)
\( f'(x)=2 \)
このように、導関数は簡単に求めることができます。
しかし、定義に従って導関数を求める場合は、「導関数の定義」を使う必要があります。
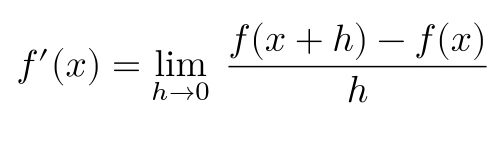
2. lim とは
導関数の定義の lim について説明します。
\( \displaystyle \lim_{ x \to 1 } x \)
リミットと読みます。リミットは英語で「極限」を意味する単語です。
リミットの下の \(x →１\) は、「\(x\) の値を限りなく \(1\) に近づける」という意味です。
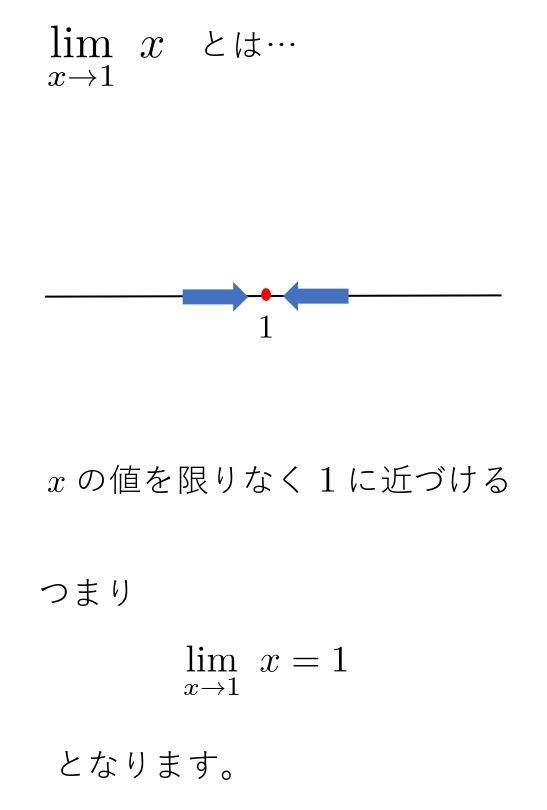
\( \displaystyle \lim_{ x \to 1 } x \)
意味は「\(x\) の値を限りなく \(1\) に近づける」
計算方法は「\(x\) に \(1\) を代入する」
となります。
3. 導関数の問題
\(定義に従って、次の導関数を求めよ。\\ \\
(1) \ \ f(x)=3x\ \ \ \ \\ \\
(2) \ \ f(x)=x^2\ \ \ \ \ \\
\)
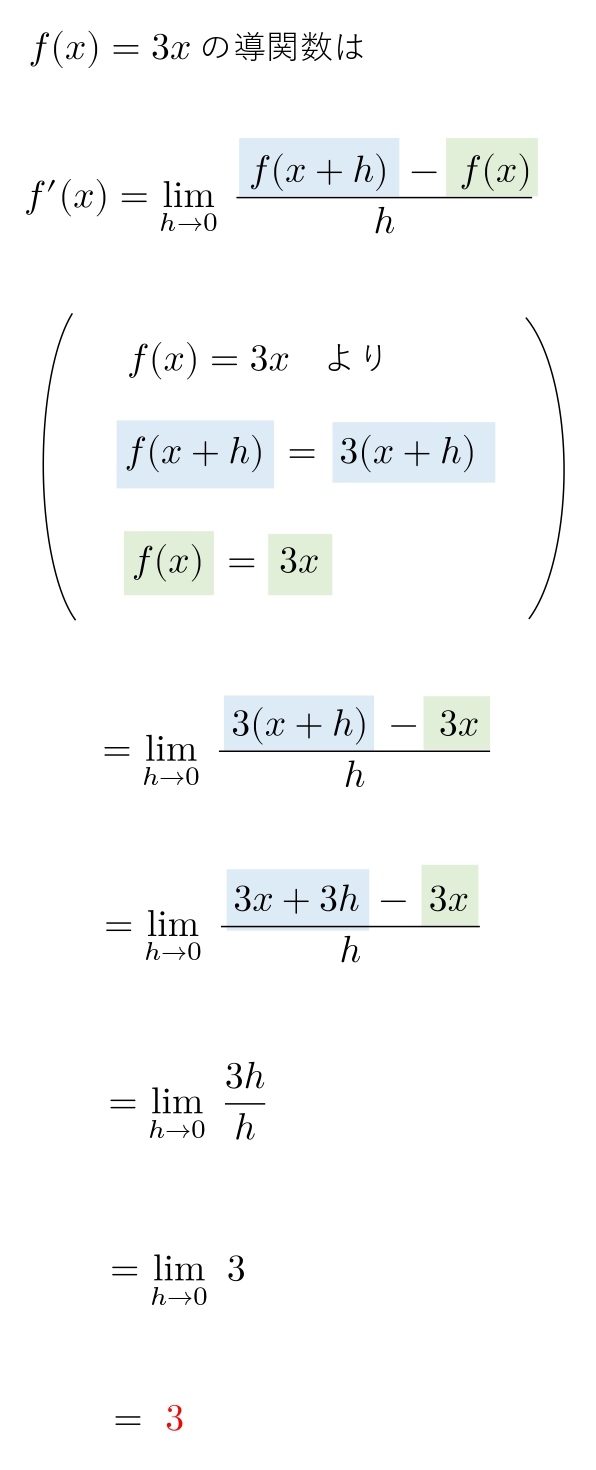
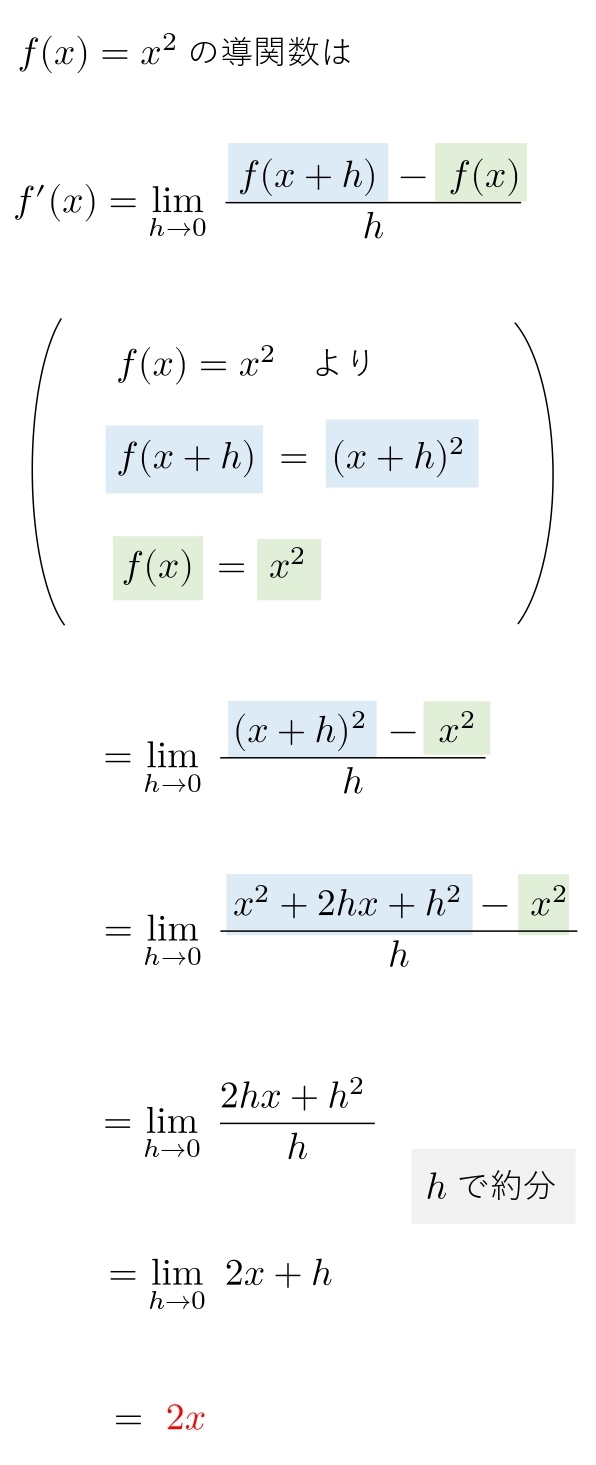
問題文に「定義に従って導関数を求めよ」と書かれていたら、このように解きます。
4. 微分法の公式一覧
数学Ⅱ「微分法」の公式一覧を、PDFファイルでA4プリント１枚にまとめました。
5. 微分法の問題
数学Ⅱ「微分法」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
