このページでは、数学Ⅰの「絶対値の外し方」について解説します。
絶対値がある方程式・不等式の公式と計算方法を，具体的に問題を解きながらわかりやすく解説していきます。基本から絶対値が２つある問題まで全部で５パターンに分けています。
問題集を解く際の参考にしてください！
目次
1. 絶対値とは
2. 絶対値の外し方①（基本）
次の値を求めよ。
\( \ \\(1) |-6|\\ \\
(2) |5-8|\\ \\
(3) |5|-|8|\\ \\
(4) |2-\sqrt{5}|\\ \)
\( |-6|=\color{#ef5350}{6}\\ \)
\( |5-8|=|-3|=\color{#ef5350}{3}\\ \)
\( |5|-|8|=5-8=\color{#ef5350}{-3}\\ \)
\( |2-\sqrt{5}|=-(2-\sqrt{5})=\color{#ef5350}{\sqrt{5}-2}\\ \)
3. 絶対値の外し方②（基本）
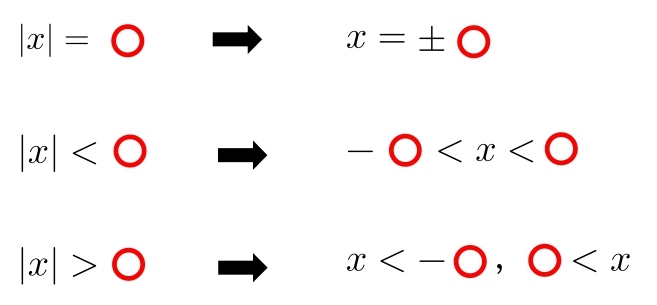
公式に当てはめるだけです。
次の方程式，不等式を解け。
\( \ \\(1) |x|=2\\ \\
(2) |x|<5\\ \\
(3) |x|≧4\\ \)
\( |x|=2\\ \\
|x|=\color{#ef5350}{\pm2}\\ \)
\( |x|<5\\ \\
\color{#ef5350}{-5<x<5}\\ \)
\( |x|≧4\\ \\
\color{#ef5350}{x≦-4，\ 4≦x}\\ \)
4. 絶対値の外し方③（基本）
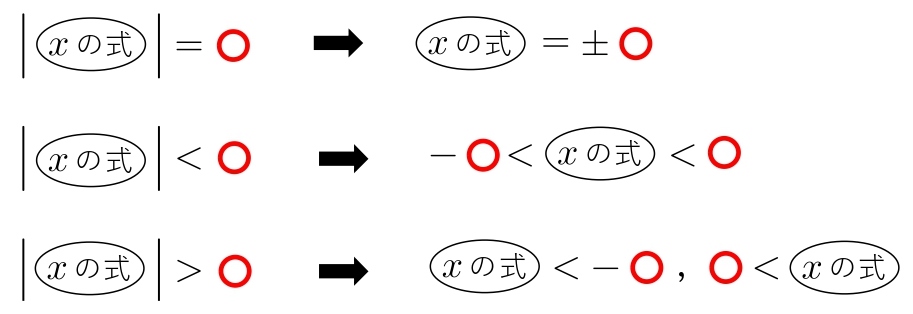
前の問題の「\(x\)」が「\(x\) の式」になっただけです。
次の方程式，不等式を解け。
\( \ \\(1) |x+4|=2\\ \\
(2) |x+4|<1\\ \\
(3) |x-2|≧1\\ \)
\( |x+4|=2\\ \\
x+4=\pm2\\ \\
\hspace{ 23pt }=-4\pm2\\ \\
\hspace{ 5pt }\color{#ef5350}{x=-2，-6}\\ \)
\( |x+4|<1\\ \\
-1<x+4<1\\ \\
\hspace{ 5pt }\color{#ef5350}{-5<x<-3}\\ \)
\( |x-2|≧1\\ \\
\hspace{ 5pt }x-2≦-1，1≦x-2\\ \\
\hspace{ 5pt }\color{#ef5350}{x≦1，\ 3≦x}\\ \)
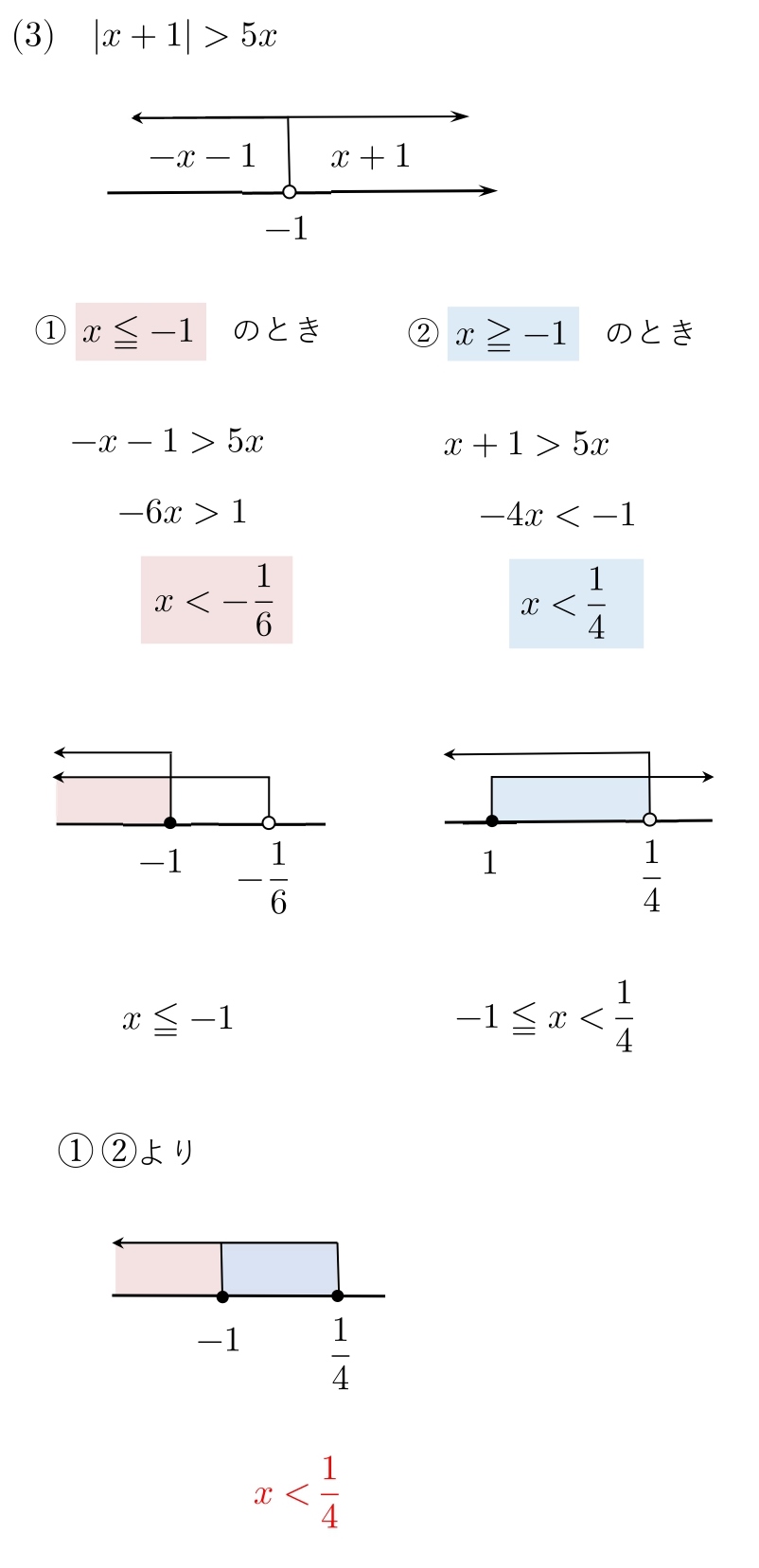
5. 絶対値の外し方④（応用）
次の方程式，不等式を解け。
\( \ \\(1) |x-3|=2x\\ \\
(2) |x-4|≦2x+1\\ \\
(3) |x+1|>5x\\ \)
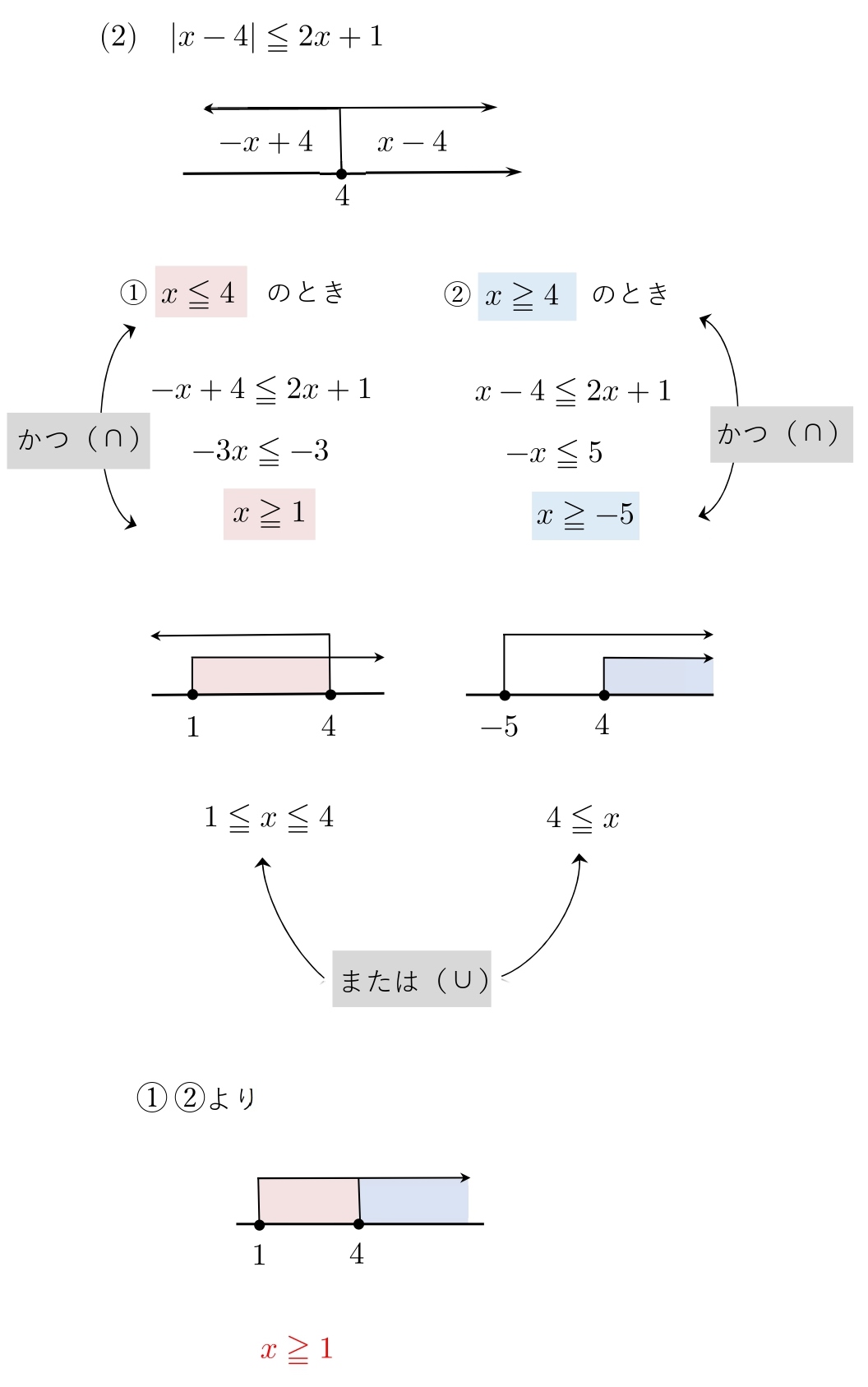
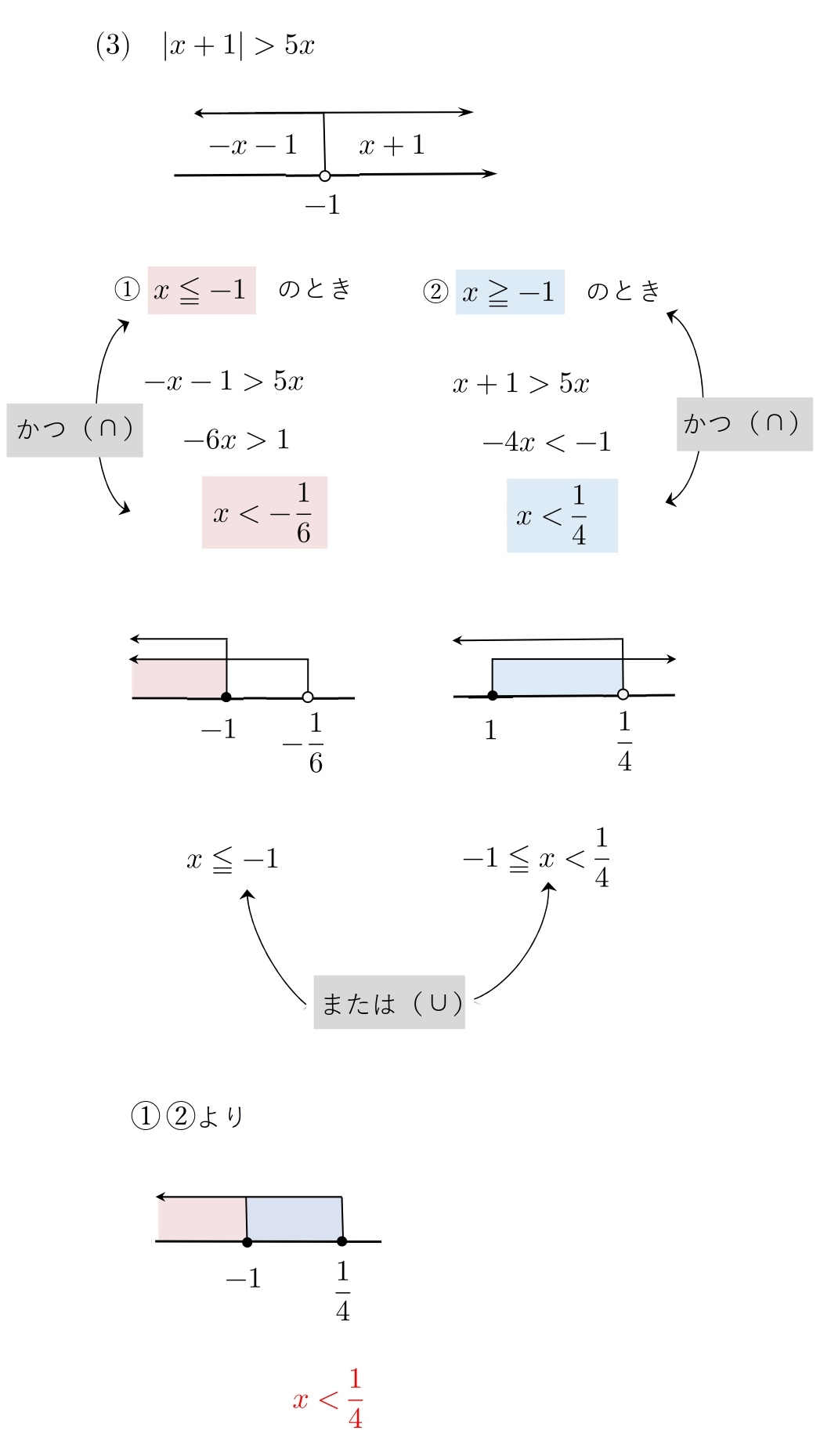
6. 絶対値が２つあるときの外し方（応用）
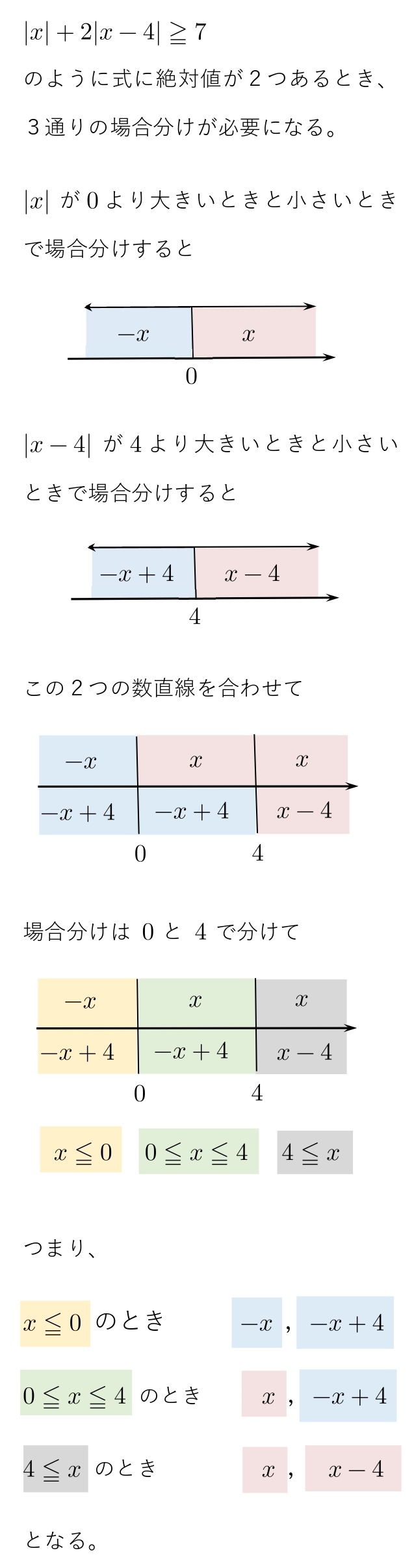
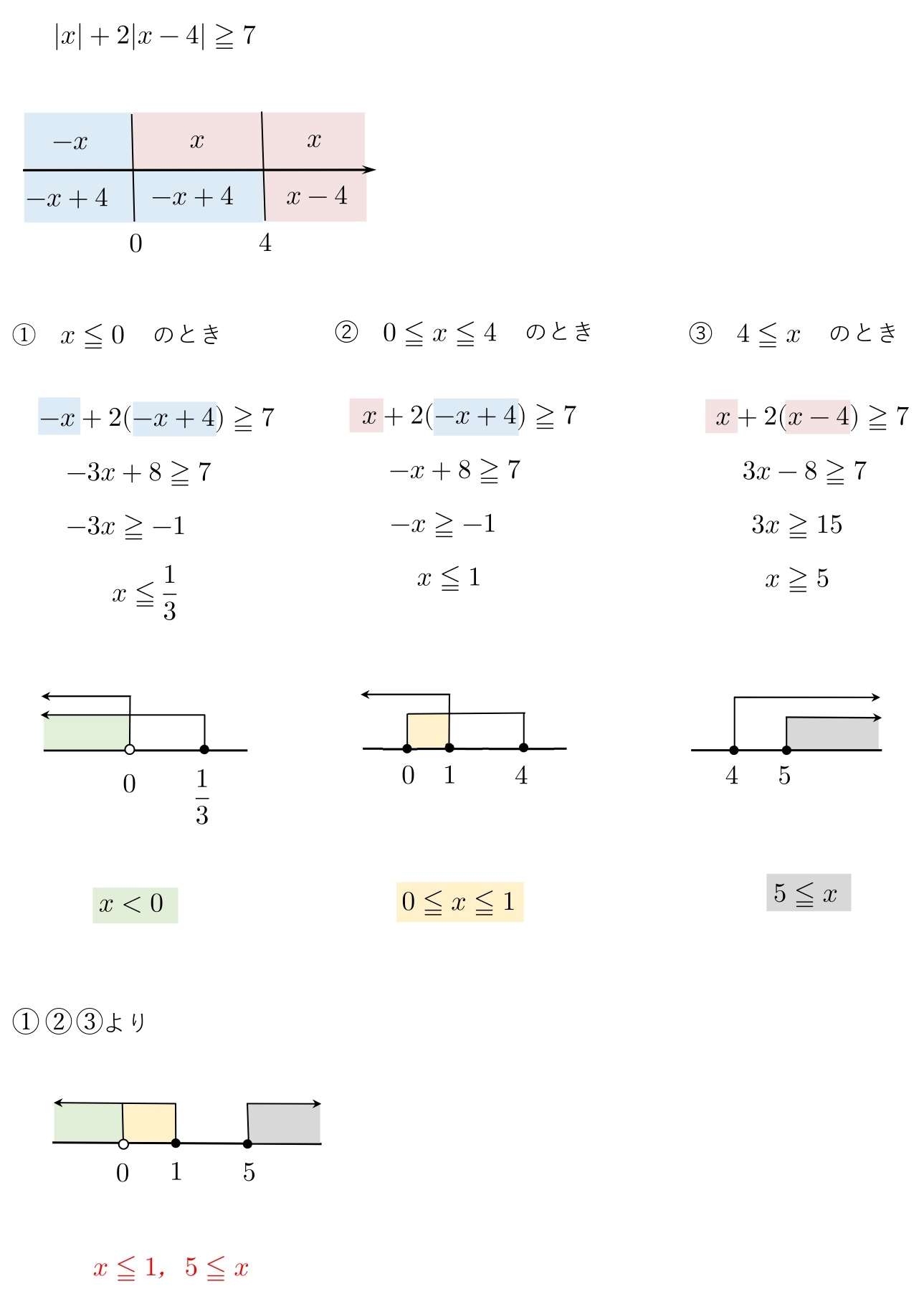
次の不等式を解け。
\( \ \\ \hspace{10pt }|x|+2|x-4|≧7\\ \)
7. 公式まとめ
数学Ⅰ「数と式」で使う公式をPDF（A4）にまとめました。
演習の際にご活用ください。
8. 絶対値の問題一覧
数学Ⅰ「絶対値」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
