このページでは、数学Ⅱの「整式の除法による余りの求め方」をまとめました。
整式の除法とは、整式同士の割り算のことです。
整式の除法による余りの求め方は、筆算、剰余の定理、組立除法の３パターンあります。
それぞれの公式と計算方法を，具体的に問題を解きながらわかりやすく解説していきます。
問題集を解く際の参考にしてください！
1. 余りの求め方の使い分け
2. 余りの求め方
2.1 筆算
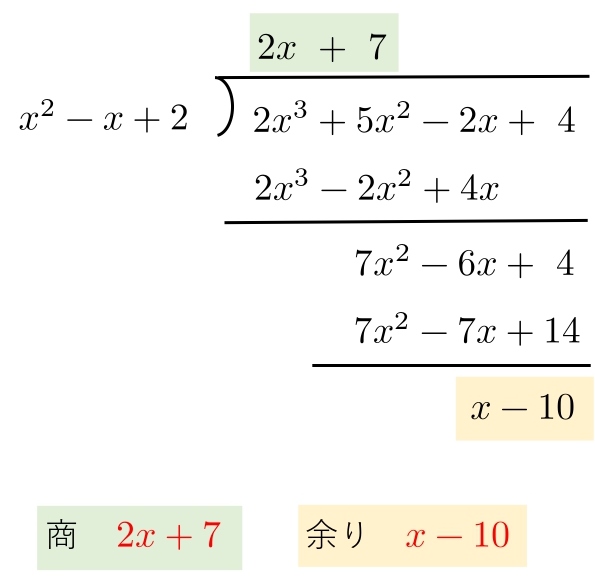
次の整式 \(A，B\) について，\( A \) を \( B \) で割った商と余りを求めよ。
\( \ \\(1) A=2x^3+5x^2-2x+4，\ \ B=x^2-x+2\\ \\
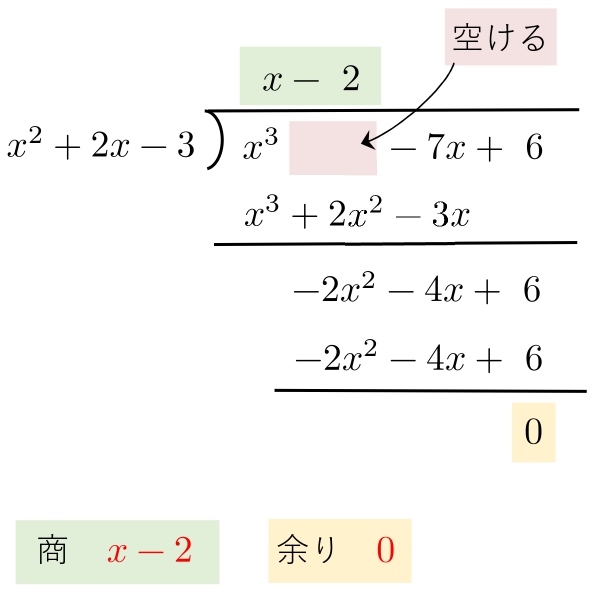
(2) A=x^3-7x+6，\ \ B=x^2-3+2x\\ \)
2.2 剰余の定理
\( P(x)=x^3+x^2-3x-2 \) を次の 1 次式で割った余りを求めよ。
\( \ \\(1) x-2\\ \\
(2) x+1\\ \\
(3) 2x-1\\ \)
\( P(2)=8+4-6-2\\ \\
\hspace{ 21pt }=\color{#ef5350}{4}\\ \)
\( P(-1)=-1+1+3-2\\ \\
\hspace{ 27pt }=\color{#ef5350}{1}\\ \)
\( \displaystyle{P\left(\frac{1}{2}\right)=\frac{1}{8}+\frac{1}{4}-\frac{3}{2}-2 \\ \\
\hspace{ 33pt }=\frac{1}{8}+\frac{2}{8}-\frac{12}{8}-\frac{16}{8}\\ \\
\hspace{ 33pt }=\color{#ef5350}{-\displaystyle\frac{25}{8}}}\\ \)
2.3 組立除法
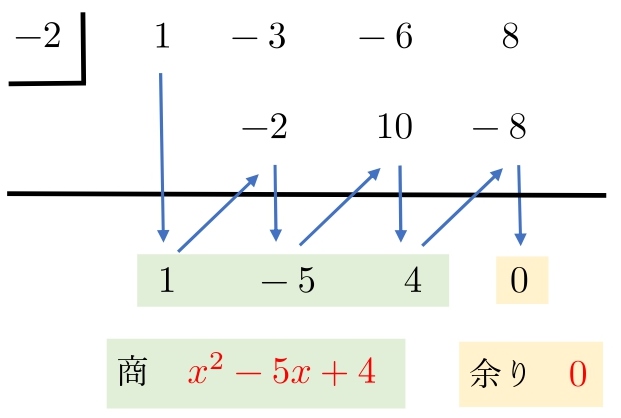
次の整式 \(A，B\) について，\( A \) を \( B \) で割った商と余りを求めよ。
\( \ \\(1) A=x^3-3x^2-6x+8，\ \ B=x+2\\ \\
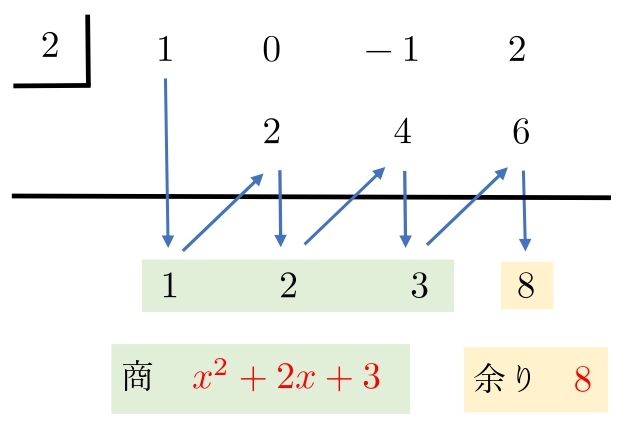
(2) A=x^3-x+2，\ \ B=x-2 \\ \)
組立除法のやり方はこちらのページで詳しく説明しているので、チェックしてみてください。
3. 公式まとめ
数学Ⅱ「複素数と方程式」の公式を、PDFファイルでA4プリント１枚にまとめました。
4. 高次方程式の問題
数学Ⅱ「複素数と方程式」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
