このページでは、数学Ⅱ「微分法」の「微分係数の定義」と「導関数の定義」をまとめました。
定義の覚え方、問題をわかりやすく解説していきます。
問題集を解く際の参考にしてください！
[toc]
1. 微分係数とは
微分係数とは接線の傾きのことです。
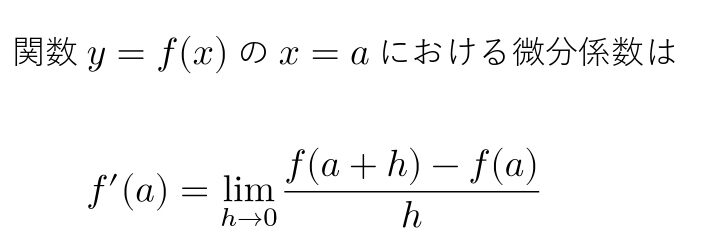
この公式は、２つの部分に分解することができます。
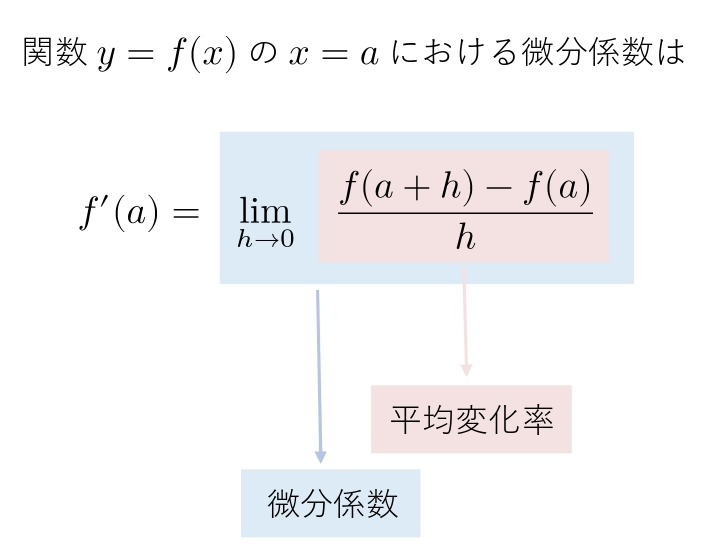
それぞれ「微分係数」「平均変化率」と言います。
平均変化率とはなんでしょうか？
2. 平均変化率とは
平均変化率とは傾きのことです。
中学では、傾き、変化の割合、 
といいました。
高校では、平均変化率といいます。
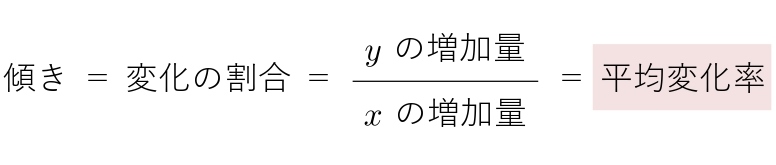
２点 \( (2，3)、(6，9)\) を結んだ赤線の傾きを見てみましょう。
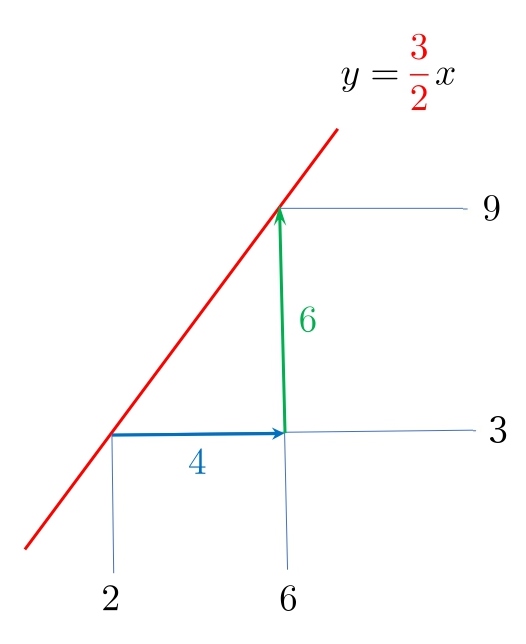
\(\color{#0000ff}{x}\) の増加量は、ヨコにどれだけ進んだか考えると \(6-2=\color{#0000ff}{4}\)
\(\color{#008000}{y}\) の増加量は、タテにどれだけ進んだか考えると \(9-3=\color{#008000}{6}\)
傾きは 
なので、 \(\displaystyle\frac{\color{#008000}{6}}{\color{#0000ff}{4}}=\color{#ef5350}{\frac{3}{2}}\) となります。
次に、 \(\displaystyle y=\frac{1}{4}x^2\) 上の２点 \(\ (2，1)、(4，4)\) の平均変化率をみてみます。
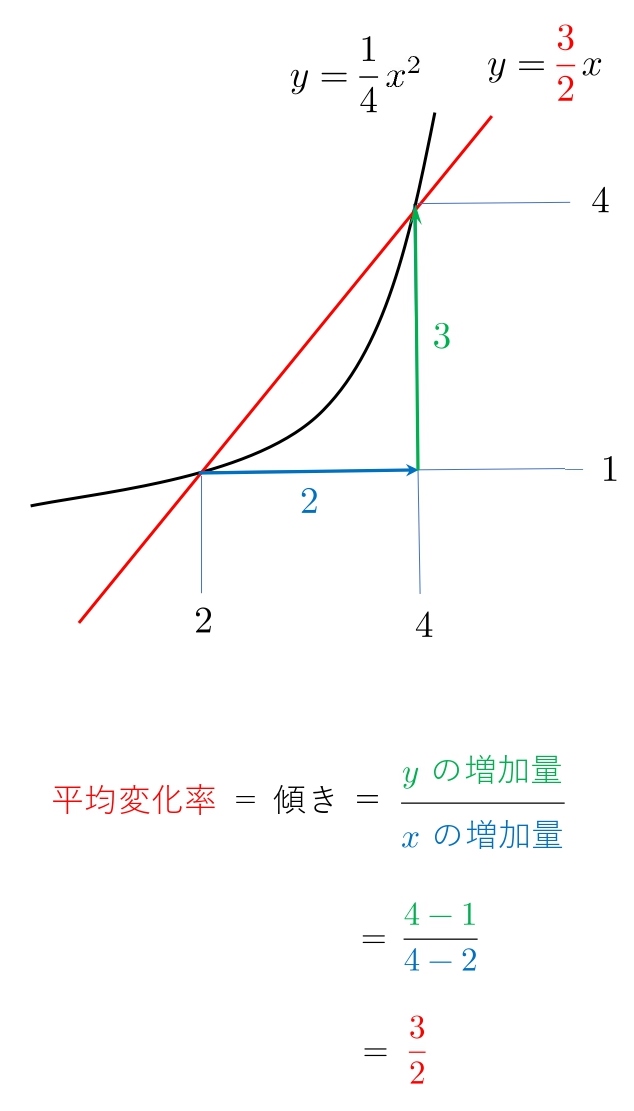
それでは 、\( y=f(x) \) のグラフに２点とって平均変化率（傾き）をみてみます。
\( y=f(x) \) は複雑に感じますが、やり方はいつもと同じです。
例えば…
\( y=x+1 \) のグラフは
\( x=1 \) のとき \( y=1+1=2 \)
\( x=3 \) のとき \( y=3+1=4 \)
\( y=f(x) \) のグラフも同様に \( x \) に値を代入します。
\( y=f(x) \) のグラフは
\( x=1 \) のとき \( y=f(1) \)
\( x=3 \) のとき \( y=f(3) \)
\( x=a \) のとき \( y=f(a) \)
\( x=a+h \) のとき \( y=f(a+h) \)
となります。
それでは 、\( y=f(x) \) 上の２点 \(\ (\ a，f(a)\ )、 (\ a+h，f(a+h)\ )\) の平均変化率（傾き）をみてみます。
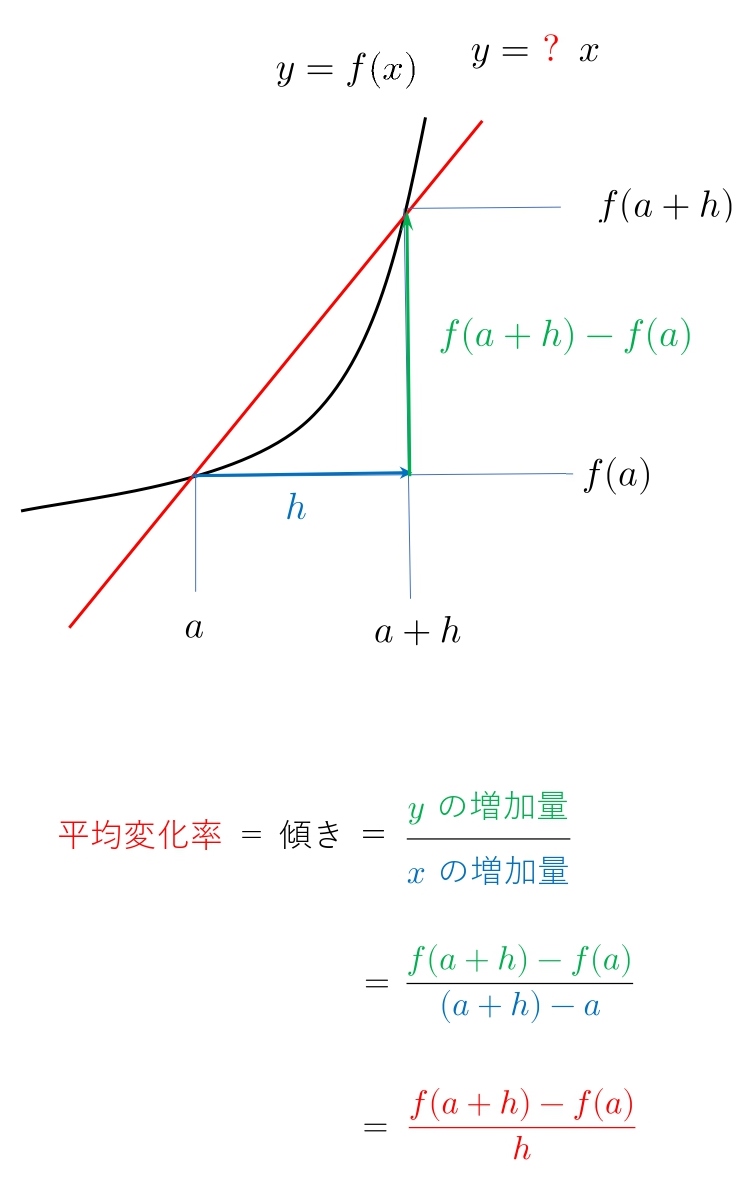
3. lim とは
微分係数の公式の lim について説明します。
\( \displaystyle \lim_{ x \to 1 } x \)
リミットと読みます。リミットは英語で「極限」を意味する単語です。
リミットの下の \(x →１\) は、「\(x\) の値を限りなく \(1\) に近づける」という意味です。
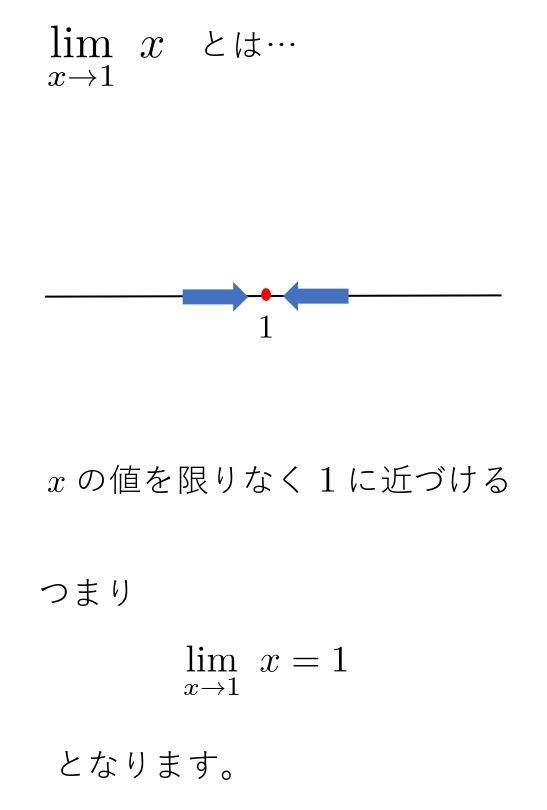
\( \displaystyle \lim_{ x \to 1 } x \)
意味は「\(x\) の値を限りなく \(1\) に近づける」
計算方法は「\(x\) に \(1\) を代入する」
となります。
4. 微分係数と接線の傾き
平均変化率、lim を説明しました。
なぜ、微分係数が接線の傾きになるのでしょうか？
このグラフの \(h\) を限りなく \(0\) に近づけていきます。
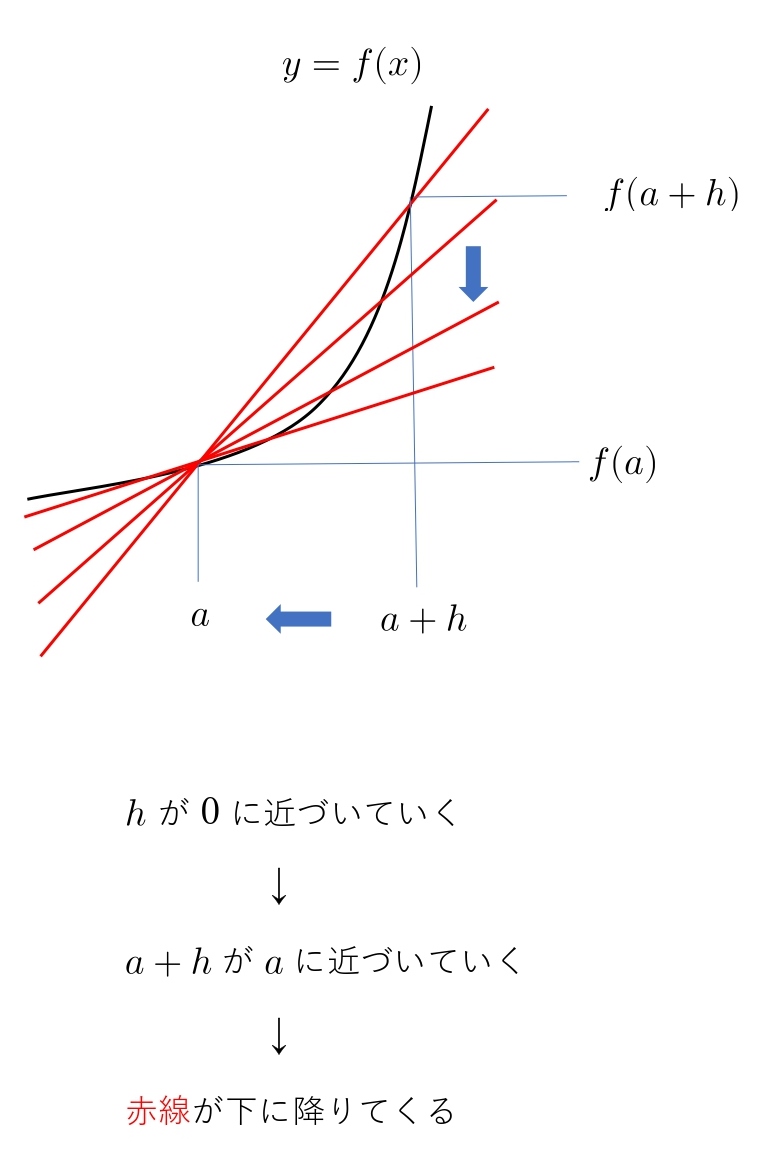
\(x\) 座標の \(a+h\) の \(h\) が \(0\) 近づいていくと、\(a+h\) は \(a\) に近づいていきます。
２点を結ぶ赤線は下に降りていきます。
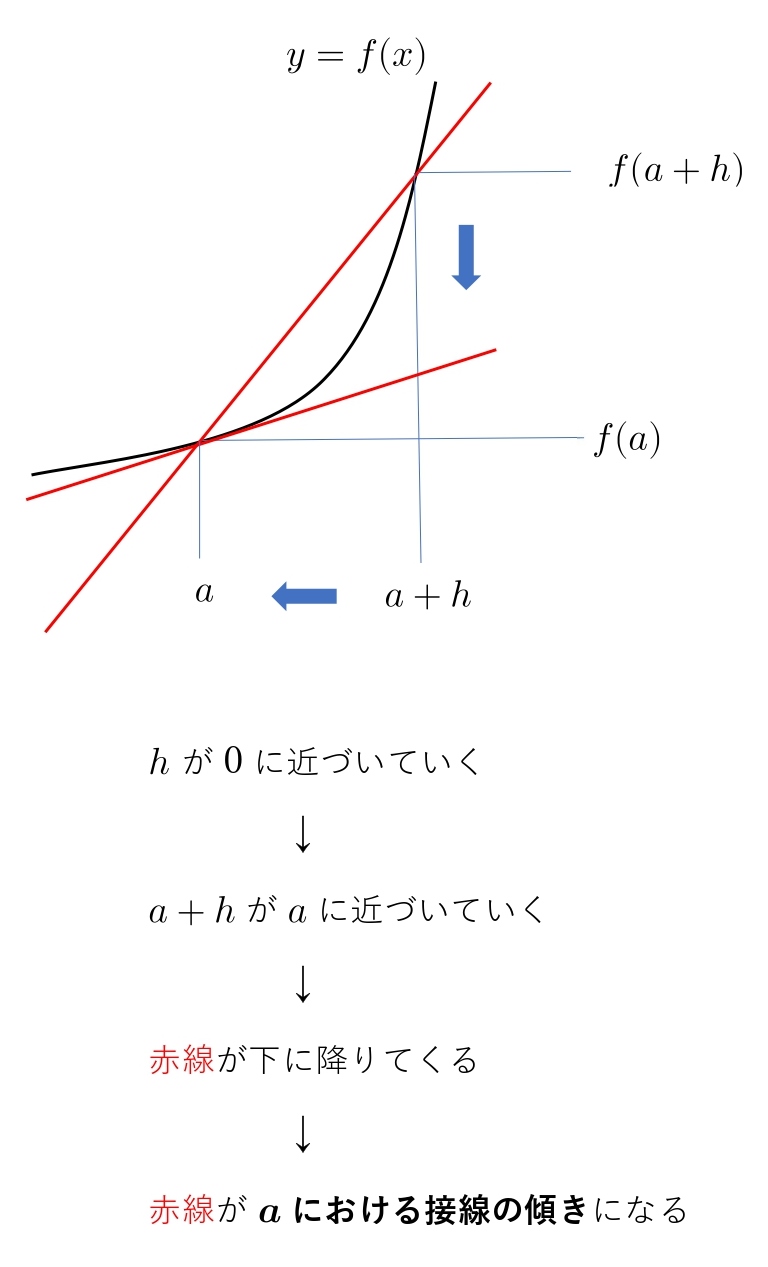
\(h\) が \(0\) に限界まで近づいたとき、赤線は \( x=a\) における接線の傾きになります。
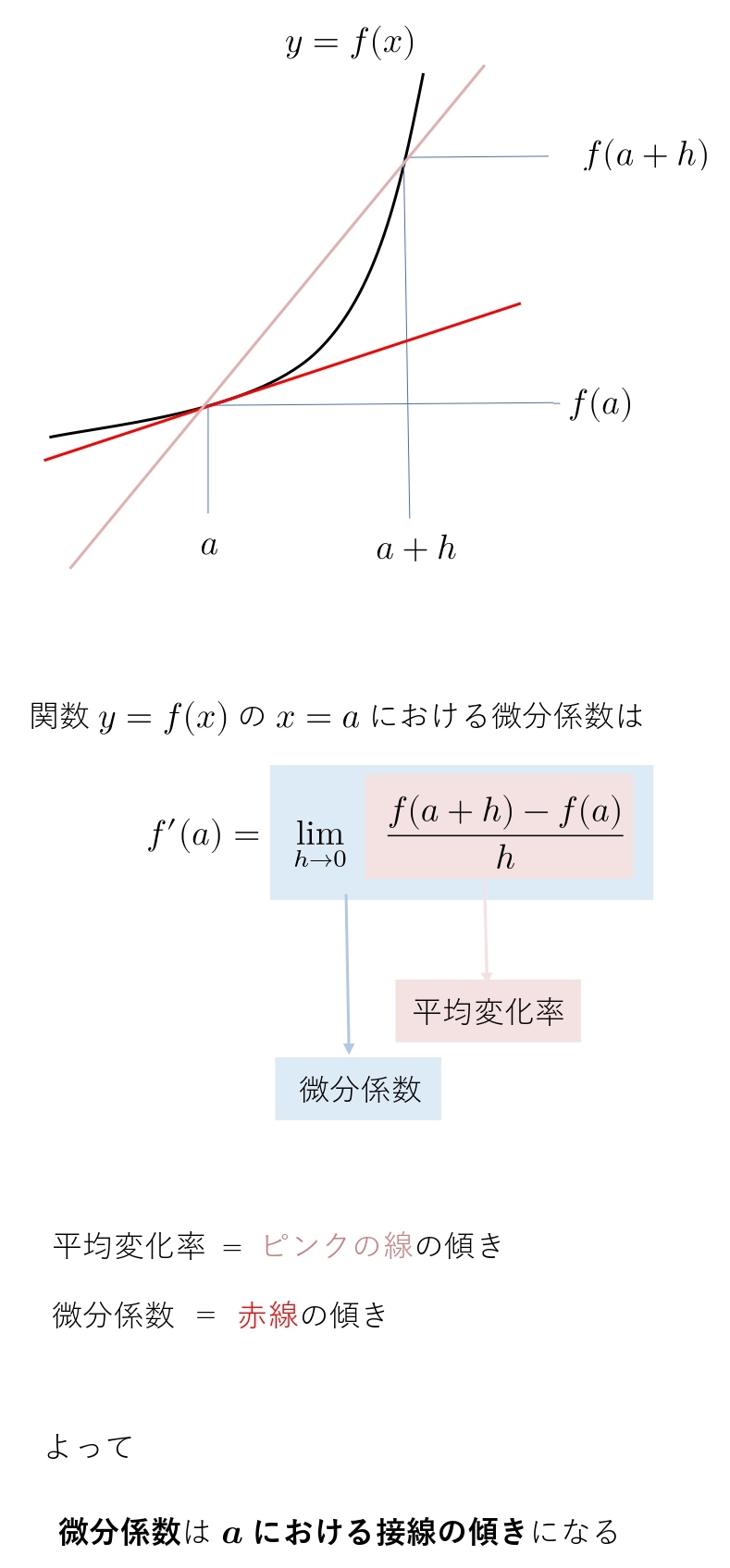
5. 微分係数の定義
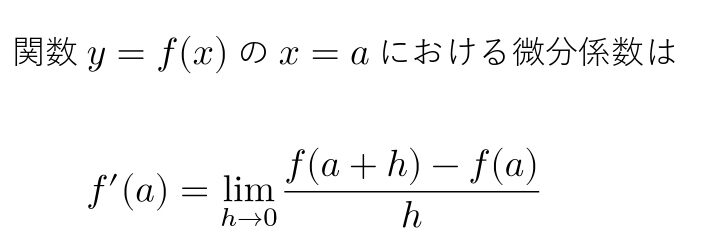
微分係数の定義に従って、問題を解いていきます。
\(定義に従って、次の\ x\ における微分係数を求めよ。\\ \\
(1) \ \ f(x)=2x-3\ \ \ \ (x=0) \\ \\
(2) \ \ f(x)=x^2\ \ \ \ \ (x=1) \\
\)
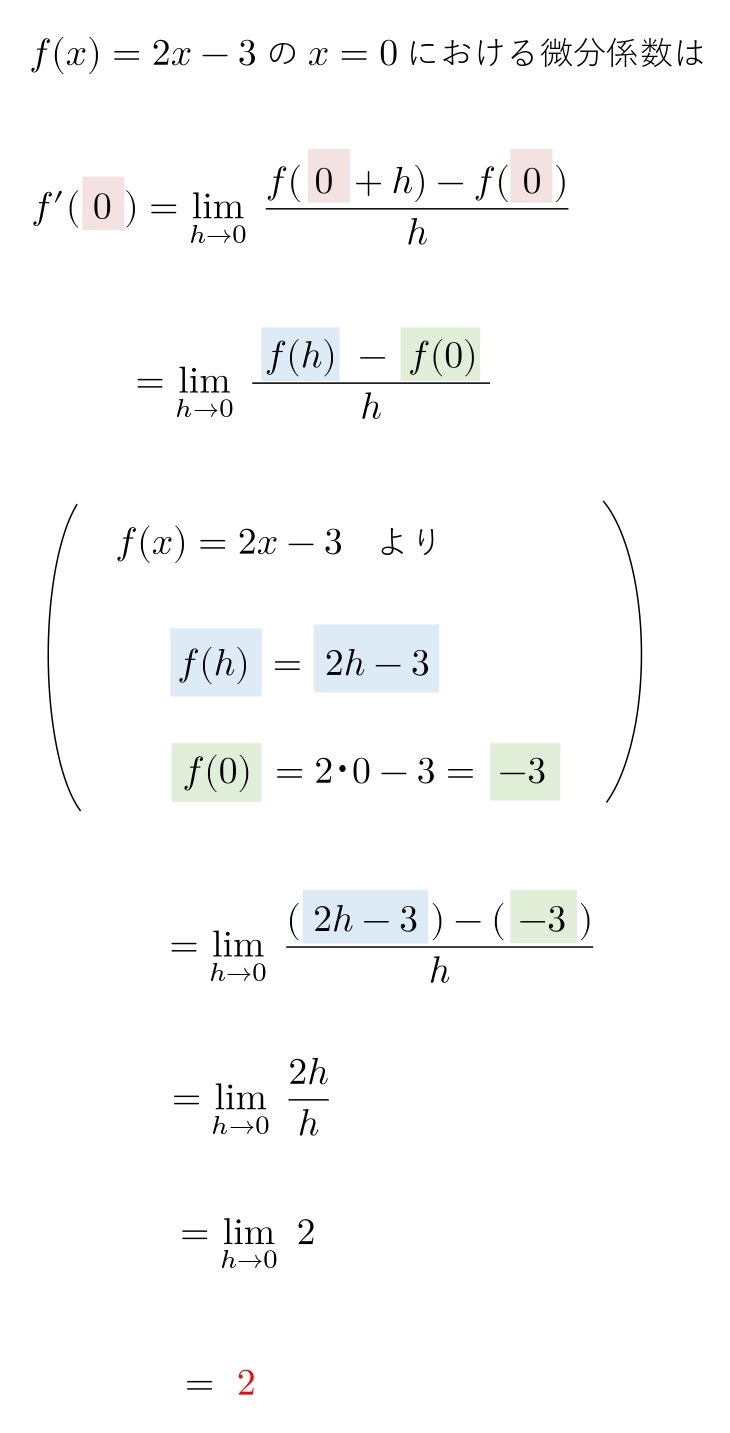
問題文に「定義に従って微分係数を求めよ」と書かれていたら、このように解きます。
6. 導関数とは
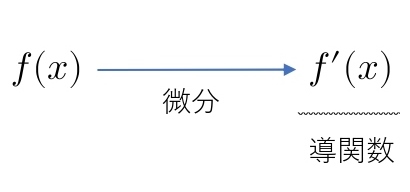
\( f(x) \) を微分したものを導関数といいます。
たとえば…
\( f(x)=2x^2+3 \)
導関数は \( f(x) \) を微分したものなので
\( f'(x)=4x \)
となります。
導関数は \( f'(x)=4x \) のように関数（文字の入った式）になります。
ただし、\( f(x) \) が１次式の場合は値
\( f(x)=2x \)
\( f'(x)=2 \)
このように、導関数は簡単に求めることができます。
しかし、定義に従って導関数を求める場合は、「導関数の定義」を使う必要があります。
7. 導関数の定義
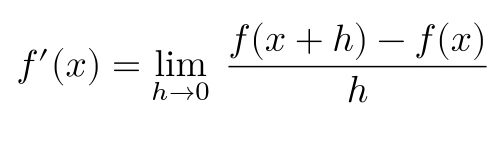
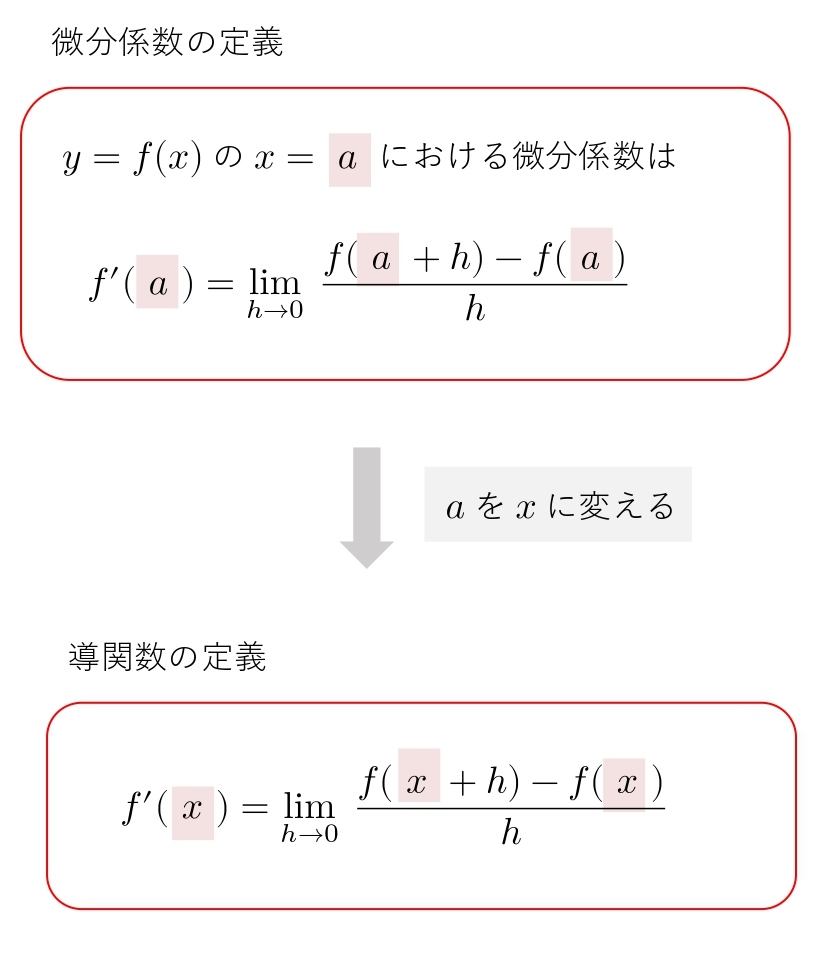
導関数の定義とは微分係数の定義の \( a \) を \( x \) に変えたものです。
実際に「導関数の定義」を使って問題を解いていきます。
\(定義に従って、次の導関数を求めよ。\\ \\
(1) \ \ f(x)=3x\ \ \ \ \\ \\
(2) \ \ f(x)=x^2\ \ \ \ \ \\
\)
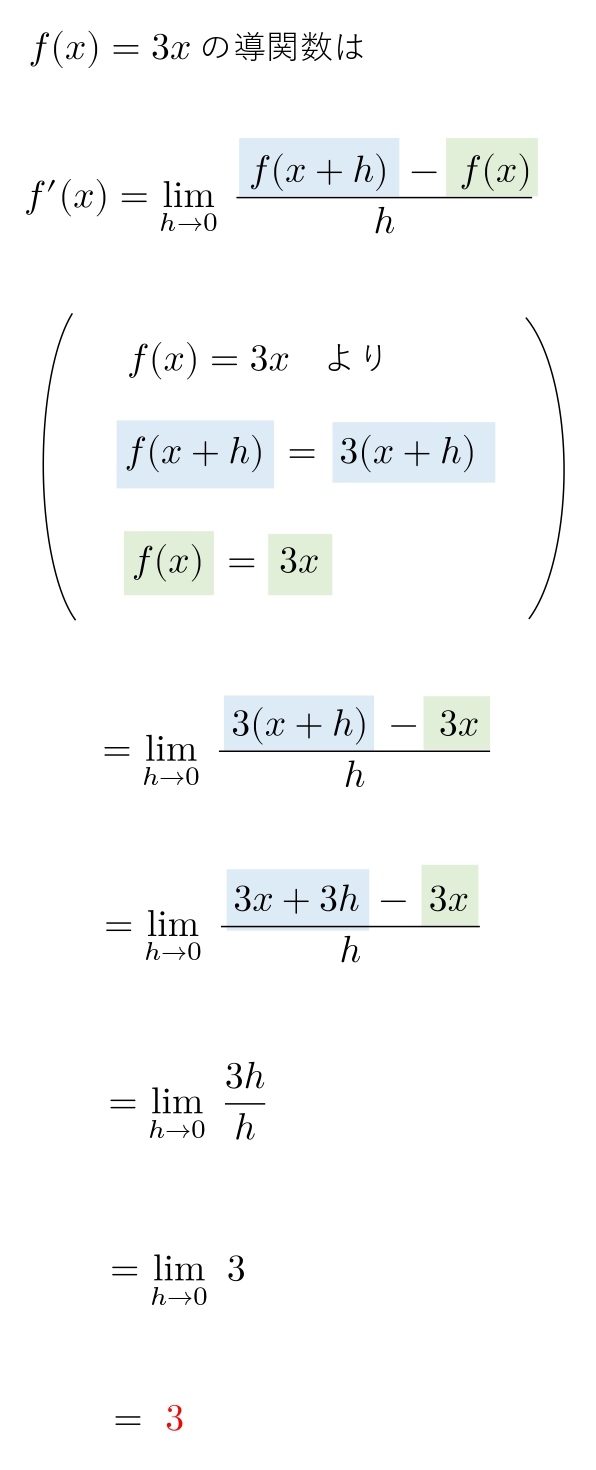
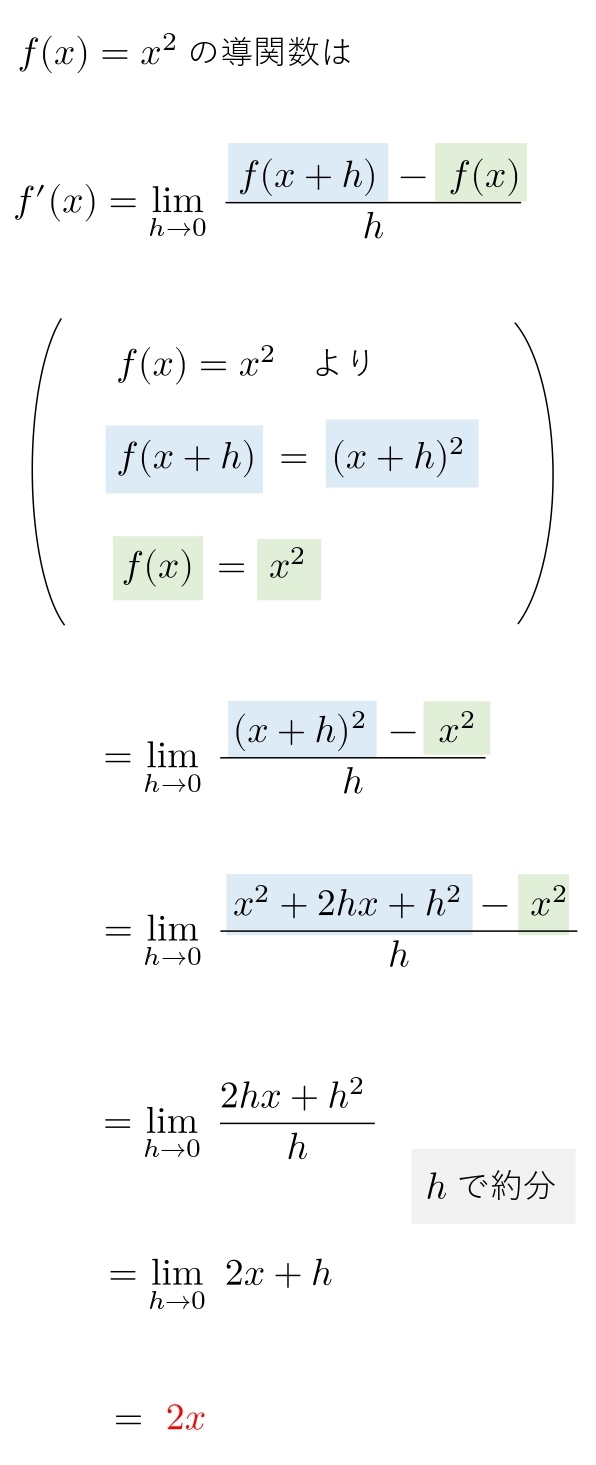
問題文に「定義に従って導関数を求めよ」と書かれていたら、このように解きます。
8. 微分係数と導関数
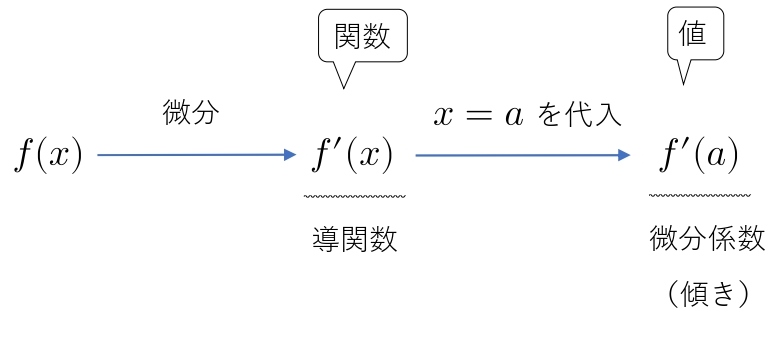
「微分係数の定義」と「導関数の定義」を使わなければ、微分係数と導関数は簡単に求めることができます。
\( f(x) \) を微分したものを導関数
導関数に \( x=a \) を代入したものを 微分係数だったので
たとえば…
\( f(x)=2x^2+3 \)
導関数は \( f(x) \) を微分するので
\( f'(x)=4x \)
\( x=2 \) における微分係数は \( x=2 \) を代入するので
\( f'(2)=8 \)
となります。
微分係数と導関数をまとめると
9. 微分法の公式一覧
数学Ⅱ「微分法」で使う公式をPDF（A4）にまとめました。
演習の際にご活用ください。
10. 微分係数の問題
数学Ⅱ「微分法」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
ぜひチェックしてみてください。
このページでは、数学Ⅱ「ô ...
【高校数学Ⅱ】微分法 教科書（問題・解答・公式・解説）