このページでは、数学Ⅱ「三角関数」の弧度法の覚え方、 sin cos tan の角度の求め方をわかりやすく解説しています。
問題集を解く際の参考にしてください！
数学Ⅰ「三角比」の sin cos tan の角度の求め方はこちらで説明しています。
目次
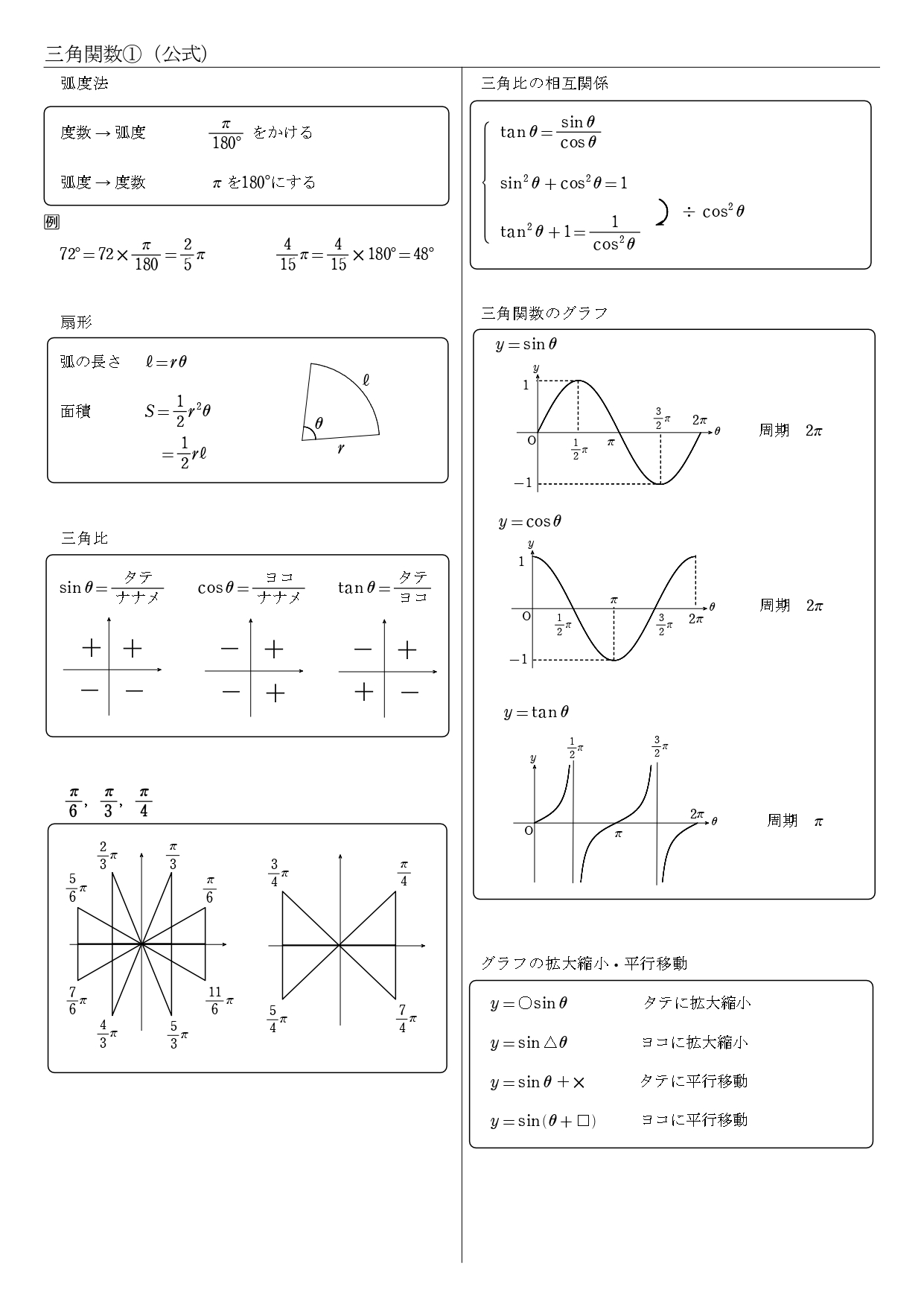
1. 弧度法
1.1 弧度法とは
\( 30° \) → \( \displaystyle{\frac{1}{6}π } \)
\( 60° \) → \( \displaystyle{\frac{1}{3}π } \)
のように、数Ⅱ「三角関数」になると、角度がπを使ったものに変わります。
\( 30°、60° \) を度数法といい、
\( \displaystyle{\frac{1}{6}π }、\displaystyle{\frac{1}{3}π } \) を弧度法といいます。
1.2 弧度法の角度
\(1、2、\sqrt3 \) の長細い三角形を使った角度を弧度法で表すと
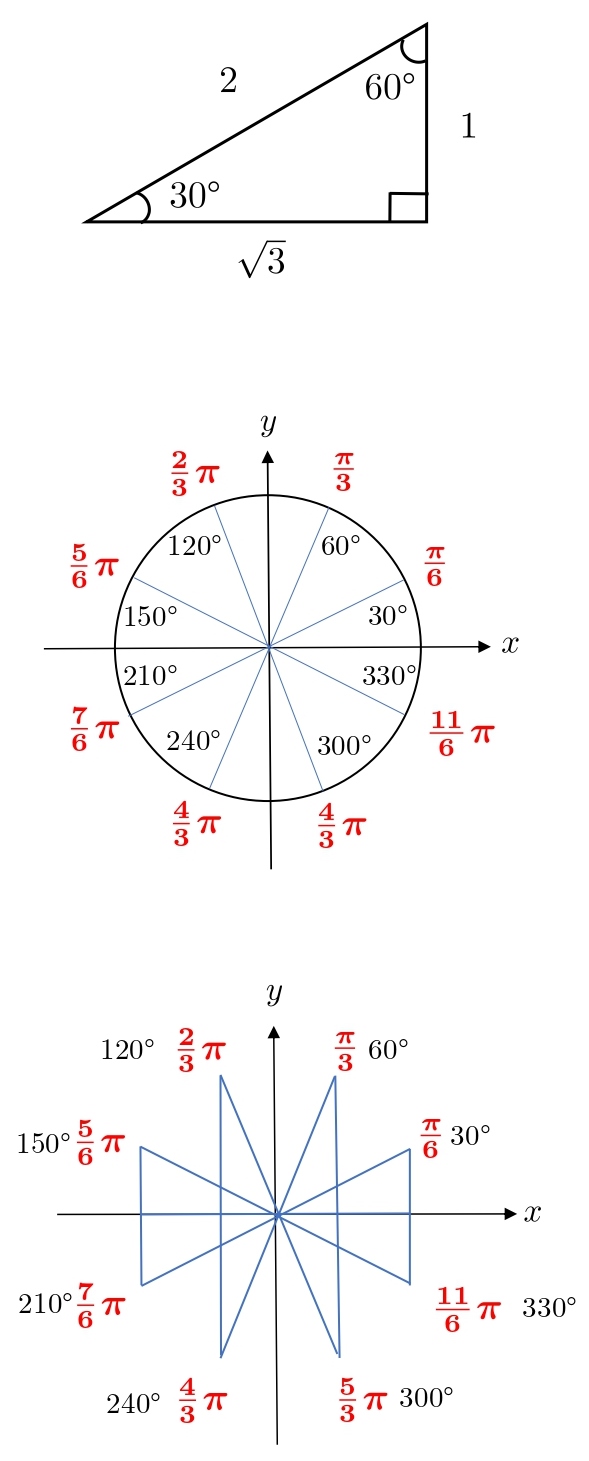
\(1、1、\sqrt2 \) の二等辺三角形を使った角度を弧度法で表すと
となります。
これらの弧度法を使った角度の覚え方を説明します。
1.3 弧度法の覚え方（\(1･2･\sqrt3 \)の三角形）
次の角度は覚えてください。
覚える必要がないという人もいますが、よく出てくるので覚えてしまったほうが楽です。
これらを覚えた前提で、第3象限、第4象限の角度を説明します。
π からどれだけ進むか、2π からどれだけ戻るか考えます。
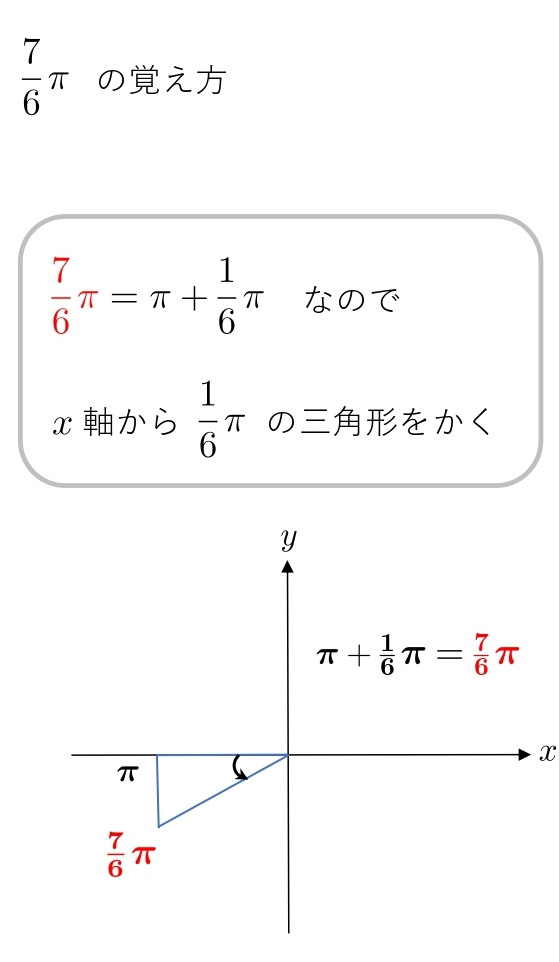
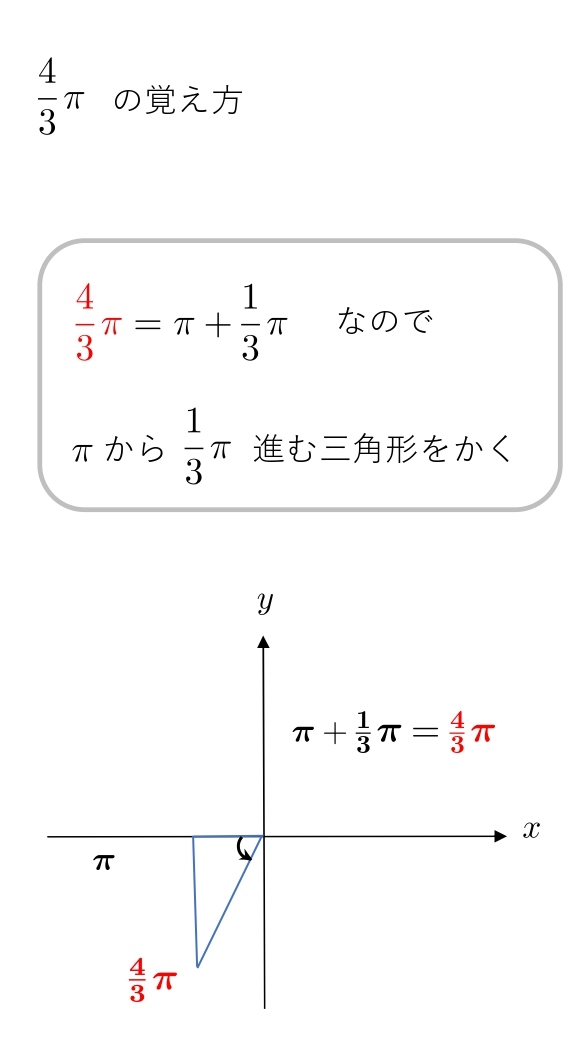
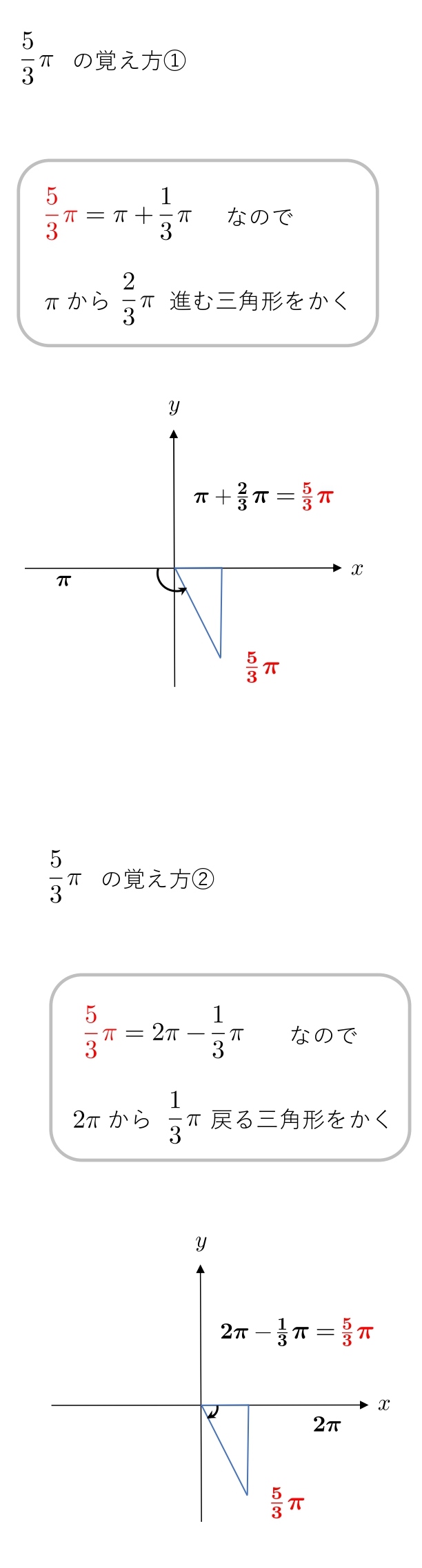
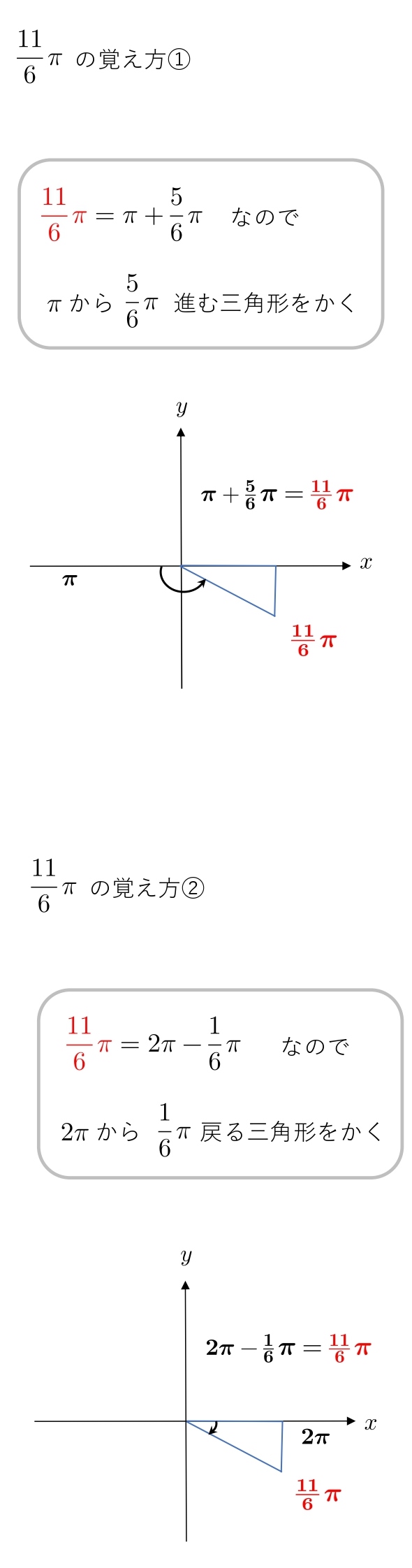
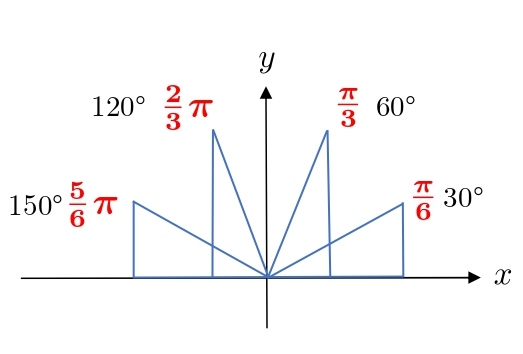
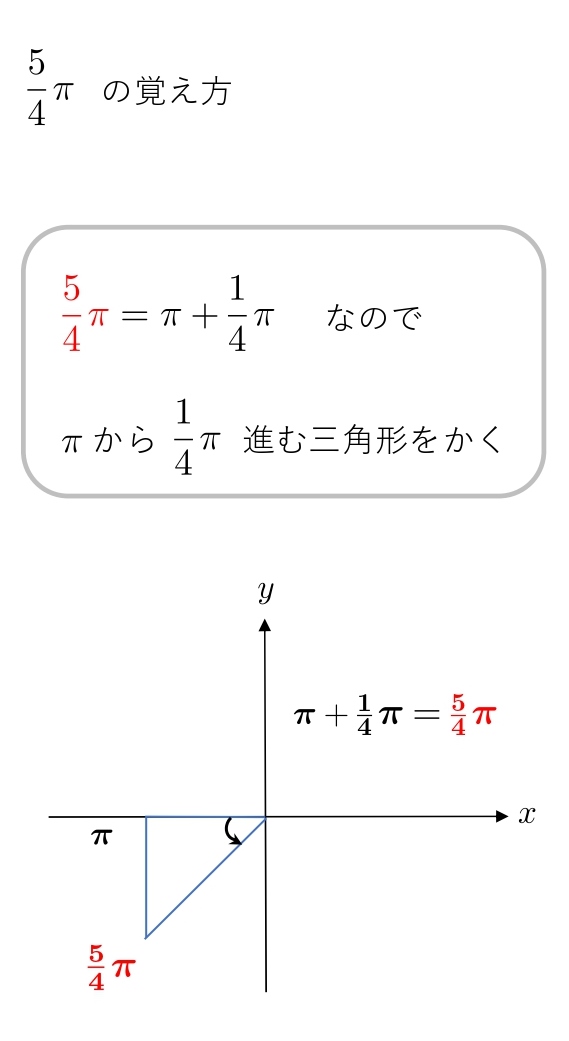
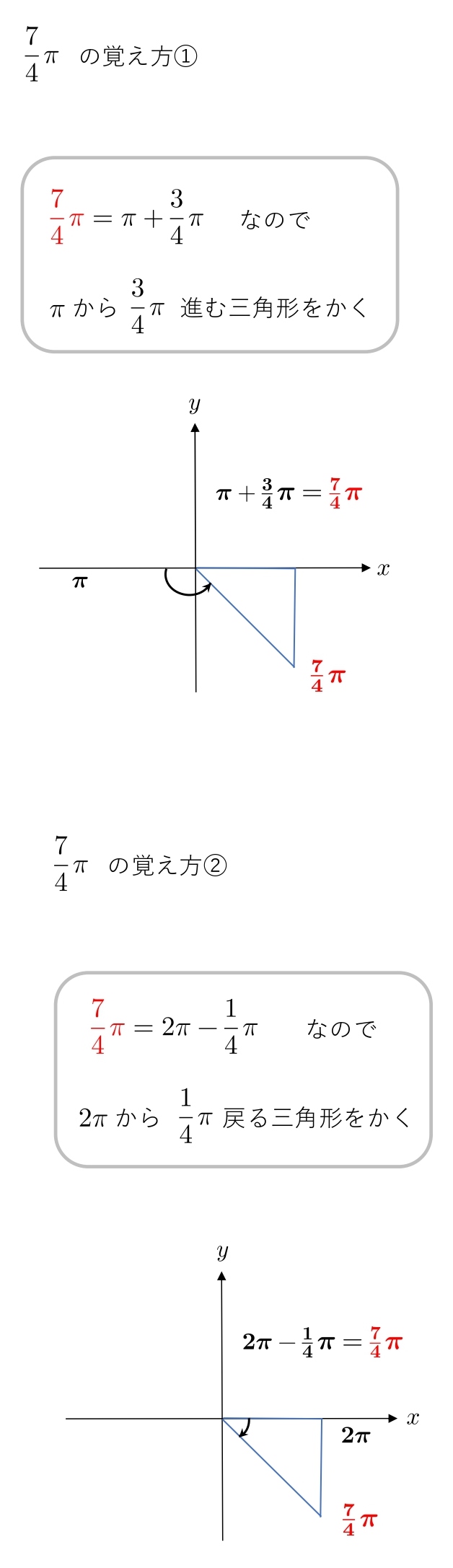
1.4 弧度法の覚え方（\(1･1･\sqrt2 \)の三角形）
\(1･2･\sqrt3 \)の三角形と同様です。
次の角度は覚えてください。
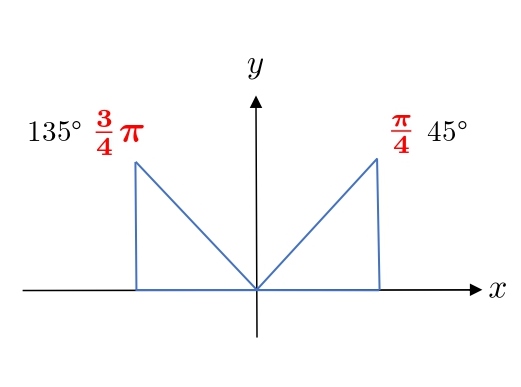
π からどれだけ進むか、2π からどれだけ戻るか考えます。
2. sin cos tan の表
sin cos tan の表はこのようになります。
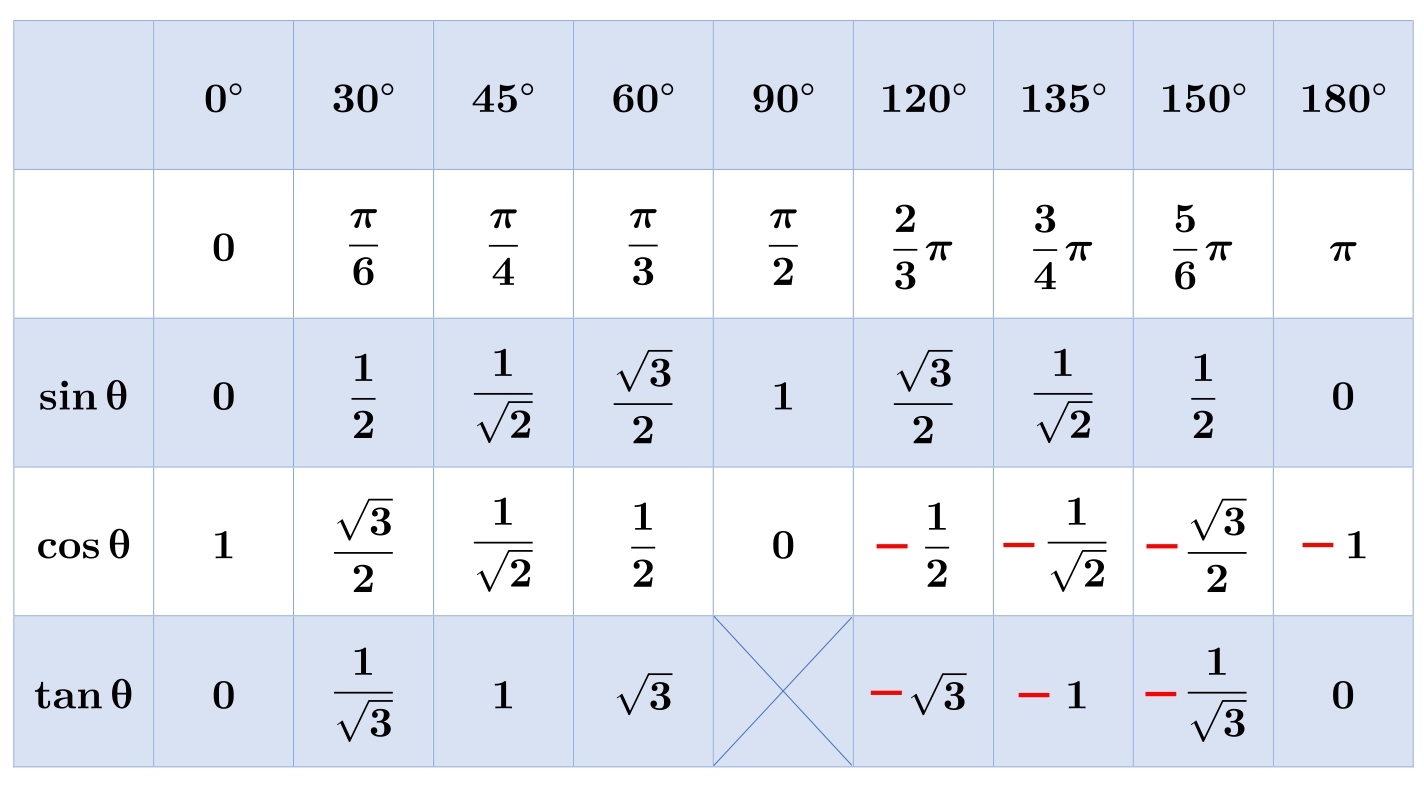
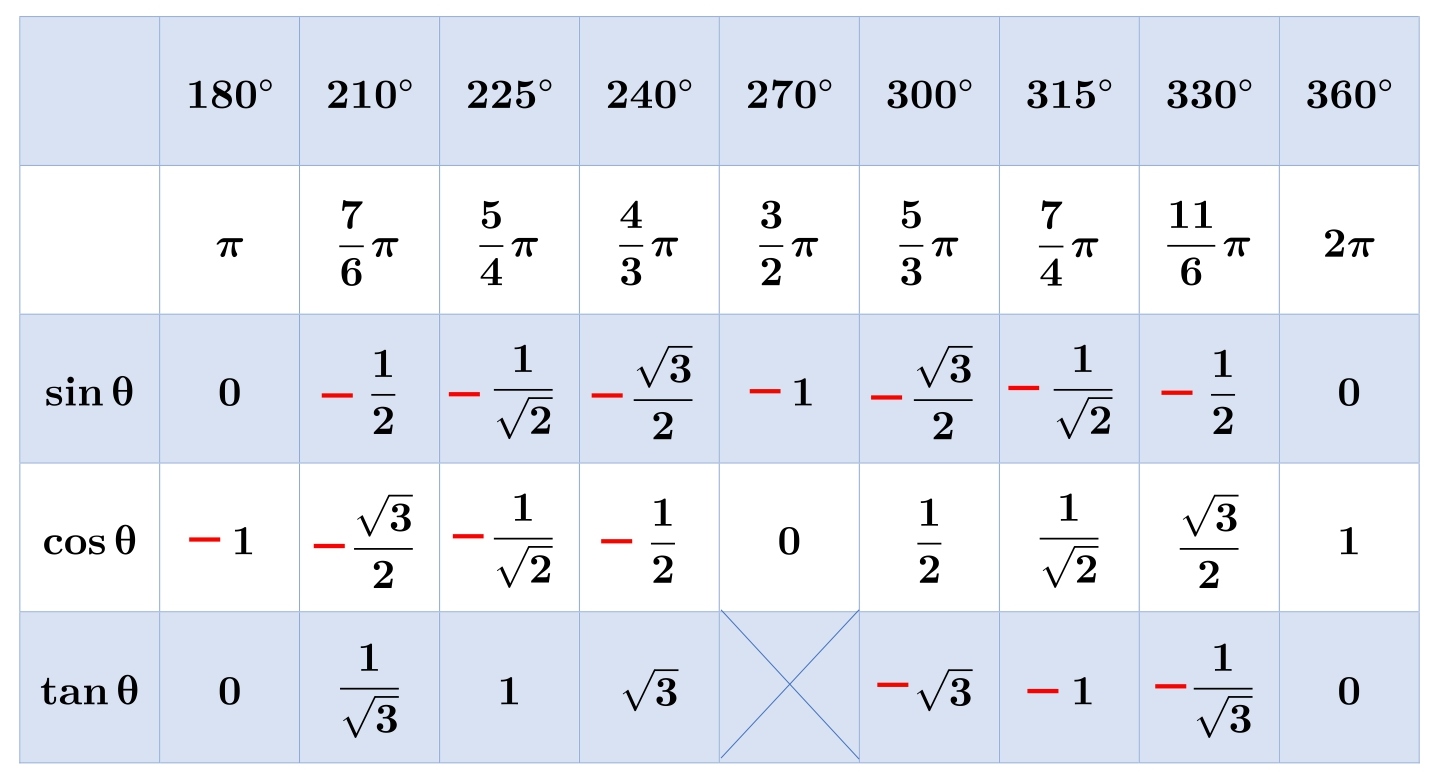
1 番左の列の \( \sinθ、 \cosθ、 \tanθ \) の \( θ \) に、角度を代入します。
たとえば…
\( \sin\displaystyle{\frac{2}{3}π}=\displaystyle{\frac{\sqrt3}{2}} \)
\( \cos\displaystyle{\frac{5}{4}π}=-\displaystyle{\frac{1}{\sqrt2}} \)
\( \tan\displaystyle{\frac{11}{6}π}=-\displaystyle{\frac{1}{\sqrt3}} \)
となります。
θを求める場合は…
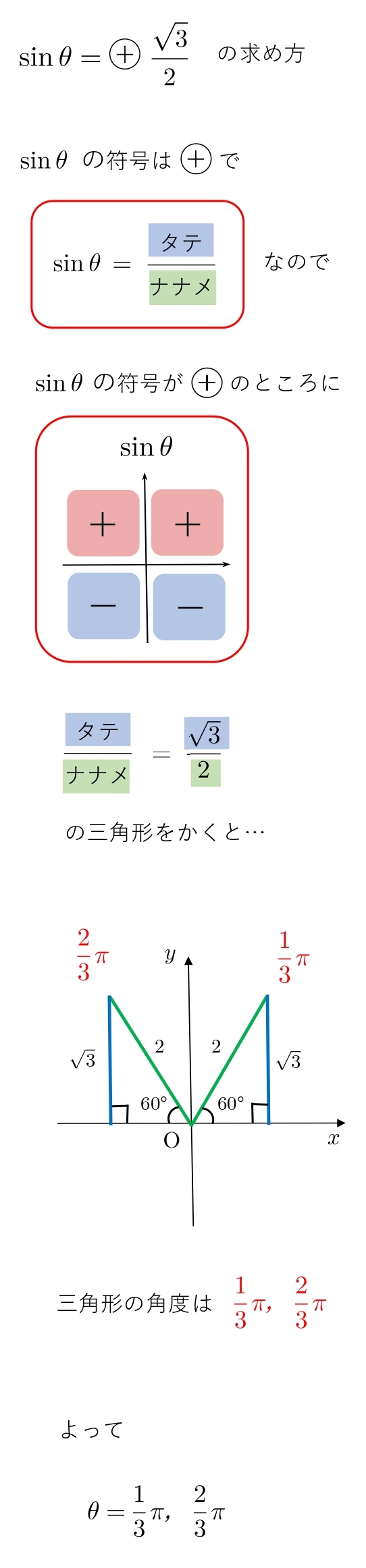
\( \sinθ=\displaystyle{\frac{\sqrt{3}}{2}} \) ならば \(θ=\displaystyle{\frac{π}{3}}，\displaystyle{\frac{2}{3}π}\)
\( \tanθ=\displaystyle{\frac{1}{\sqrt3}} \) ならば \(θ=\displaystyle{\frac{π}{6}}，\displaystyle{\frac{7}{6}π}\)
となります。
ただし、この表を覚える必要はありません。
表を覚えなくても値が求められる方法を説明します。
3. sin cos tan の表の覚え方
3.1 基礎知識
sin cos tan の値の求める前に基礎知識が必要です。
次の 3 つの公式は暗記してください。
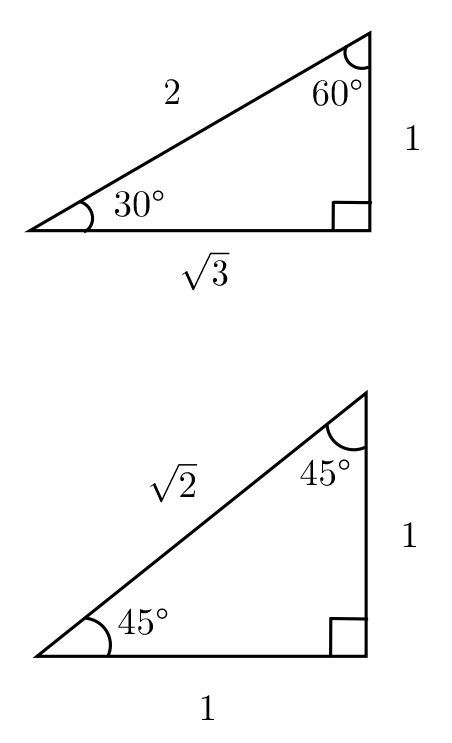
小学生のときに使った三角定規です。
角度と辺の比を覚えてください。
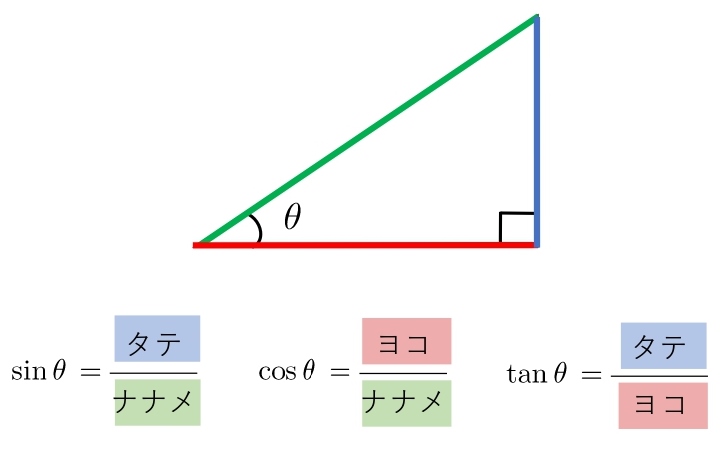
sin cos tan と三角形の比の関係です。
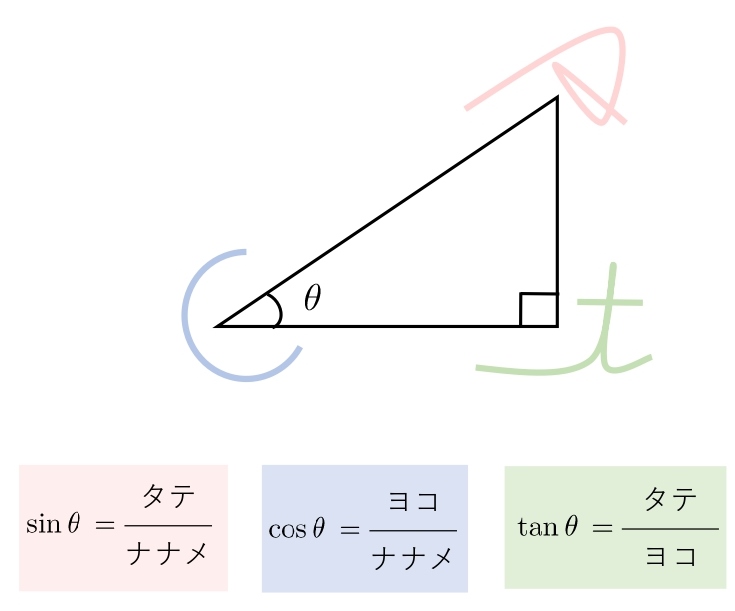
sin cos tan の 1 文字目の筆記体を「分母→分子」の順でみます。
sin の s、cos の c、tan の t を三角形の辺に沿って描くと、sin cos tan の値になります。
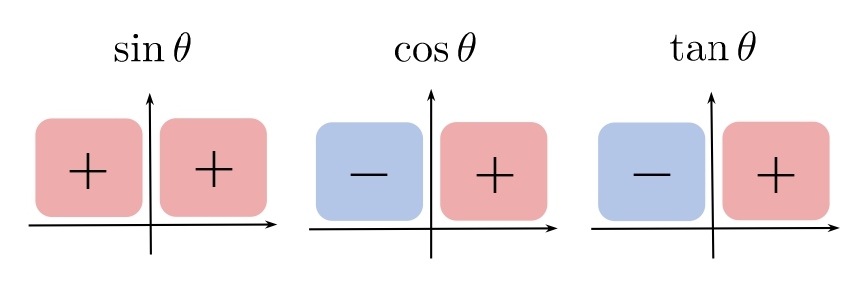
sin cos tan の符号です。
これら 3 つの公式は暗記して下さい。
この基礎知識がある前提で sin cos tan の値の求め方を説明します。
3.2 sin cos tan の値の求め方
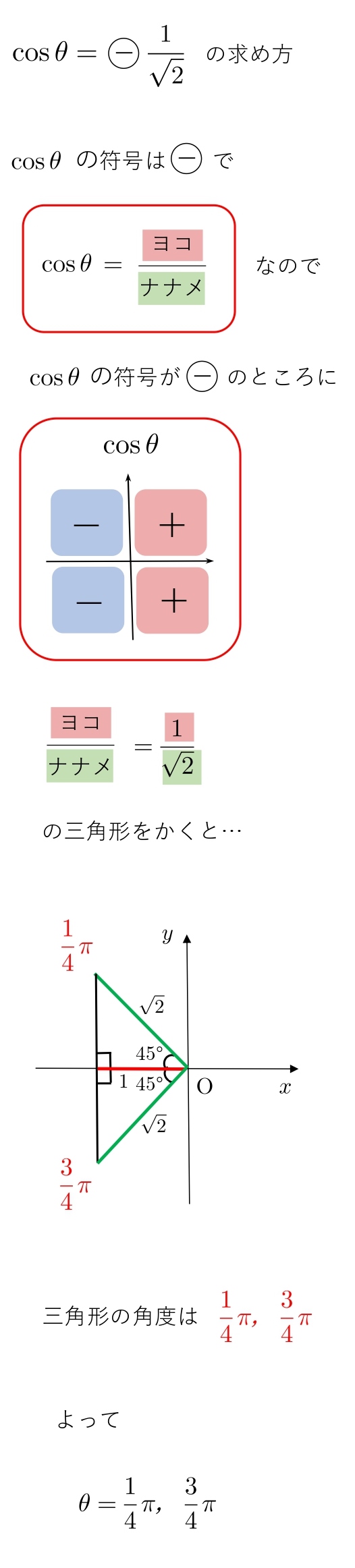
\(0≦θ\lt2π\) のとき、次の方程式を解け。
(1) \( \sinθ=\displaystyle{\frac{\sqrt{3}}{2}} \)
(2) \( \cosθ=\displaystyle{-\frac{1}{\sqrt2}} \)
数学Ⅱ「三角関数」の sin cos tan の不等式はこちらで説明しています。ぜひ、チェックしてみてください。
4. 公式まとめ
数学Ⅱ「三角関数」の公式一覧を、PDFファイルでA4プリント１枚にまとめました。
5. 三角関数の問題
数学Ⅱ「三角関数」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
