このページでは、数学Ⅰ「三角比」の sin cos tan の角度の求め方をまとめました。
問題集を解く際の参考にしてください!
数学Ⅱ「三角関数」の sin cos tan の角度の求め方はこちらで説明しています。
このページでは、数学Ⅱ「Ç ...

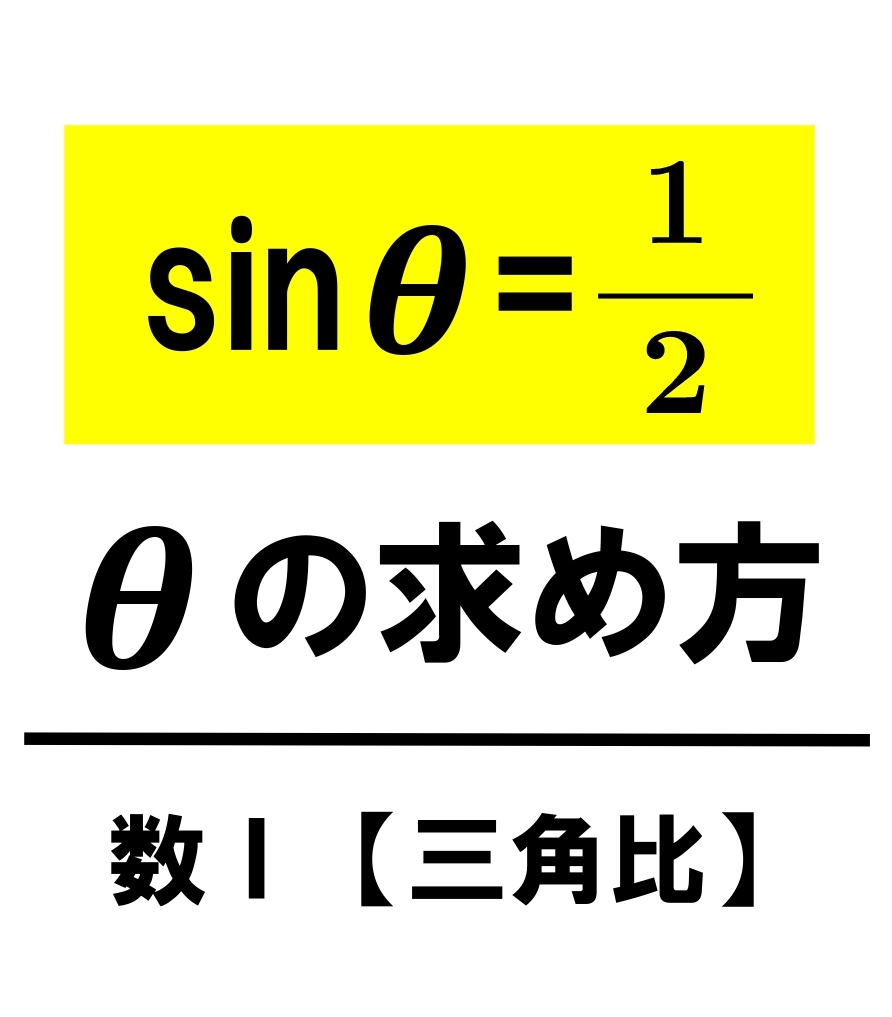
【高校数学Ⅱ】sinθ=1/2は?sin cos tan の方程式(θの求め方・計算方法)
[toc]
1. sin cos tan の表
sin cos tan の表はこのようになります。
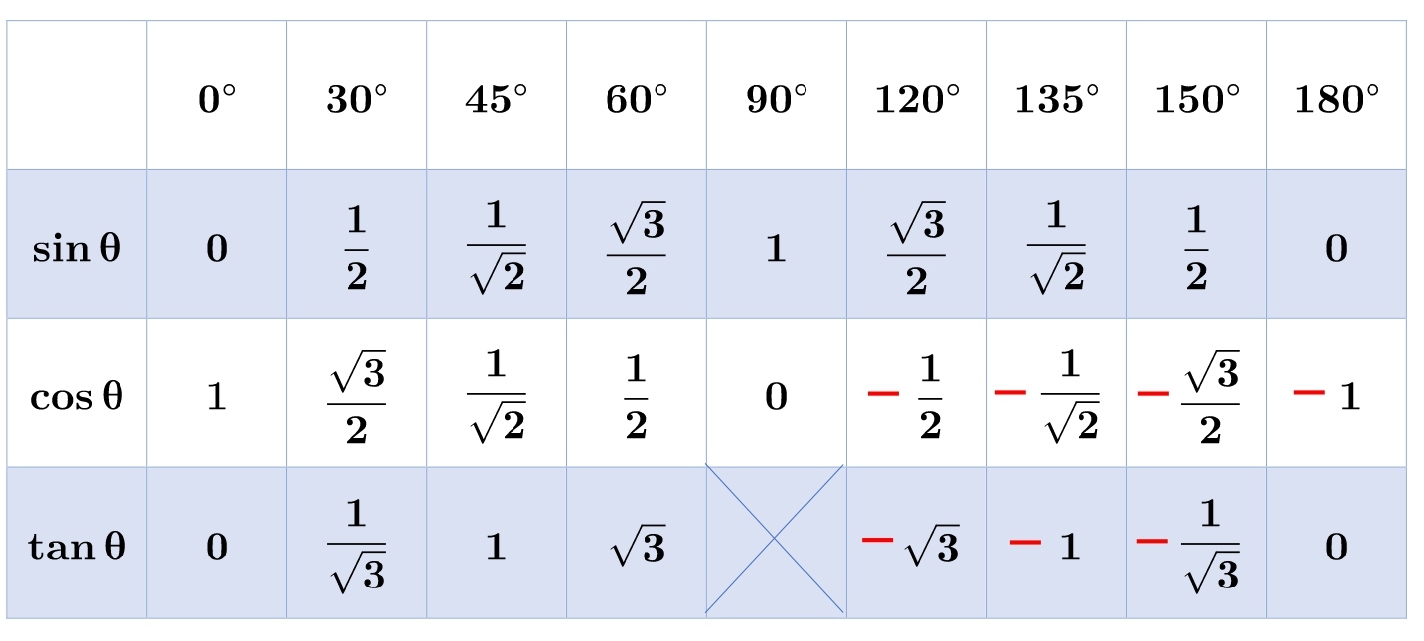
1 番左の列の \( \sinθ、 \cosθ、 \tanθ \) の \(θ\) に、1 番上の行の角度を代入します。
たとえば…
\( \sin60°=\displaystyle{\frac{\sqrt{3}}{2}} \)
\( \cos120°=\displaystyle{-\frac{1}{2}} \)
\( \tan150°=-\displaystyle{\frac{1}{\sqrt{3}}} \)
となります。
θを求める場合は…
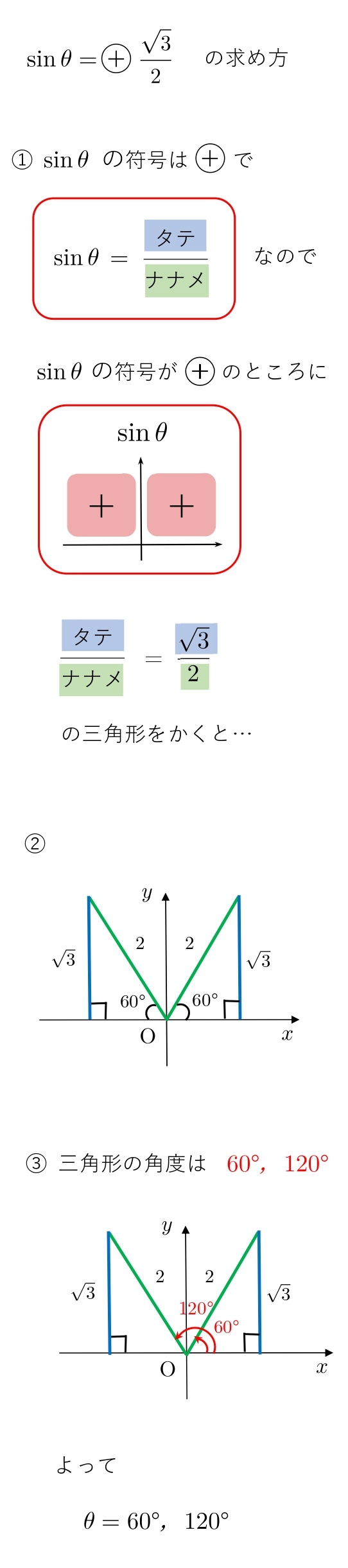
\( \sinθ=\displaystyle{\frac{\sqrt{3}}{2}} \) ならば \(θ=60°,120°\)
\( \tanθ=\displaystyle{\frac{1}{\sqrt3}} \) ならば \(θ=30°\)
となります。
これくらいの表なら暗記できそうですが、数学II「三角関数」の単元になると0°~360°まで拡張されて、覚える量が 2 倍になります。
そこで、表を覚えなくてもθが求められる方法を説明します。
2. sin cos tan のθの求め方
2.1 基礎知識
sin cos tan のθを求める前に基礎知識が必要です。
次の 3 つの公式は暗記してください。
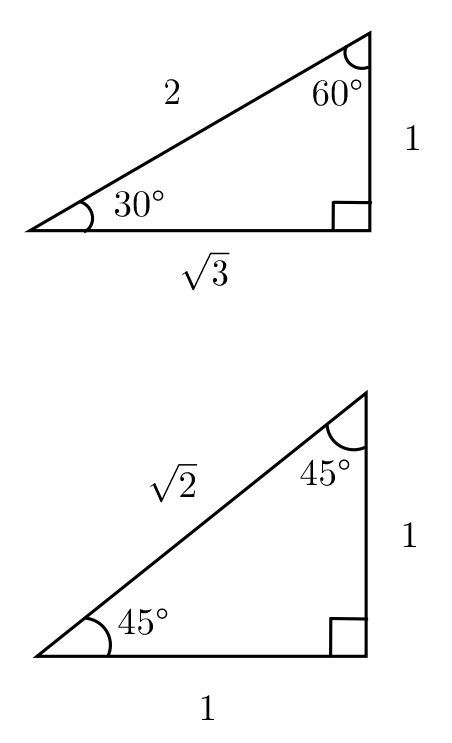
小学生のときに使った三角定規です。
角度と辺の比を覚えてください。
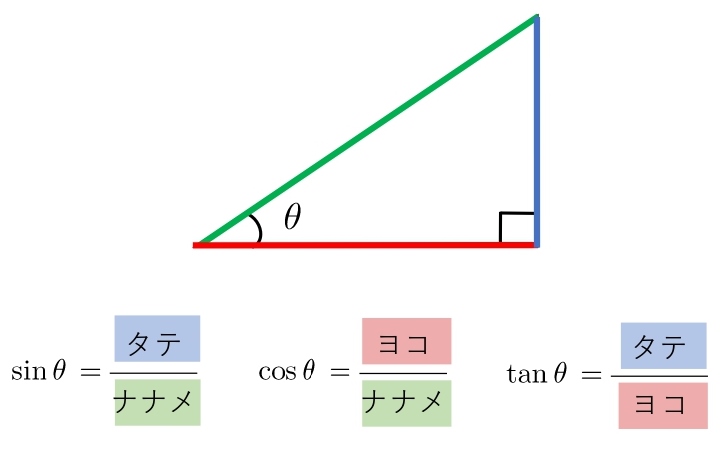
sin cos tan と三角形の比の関係です。
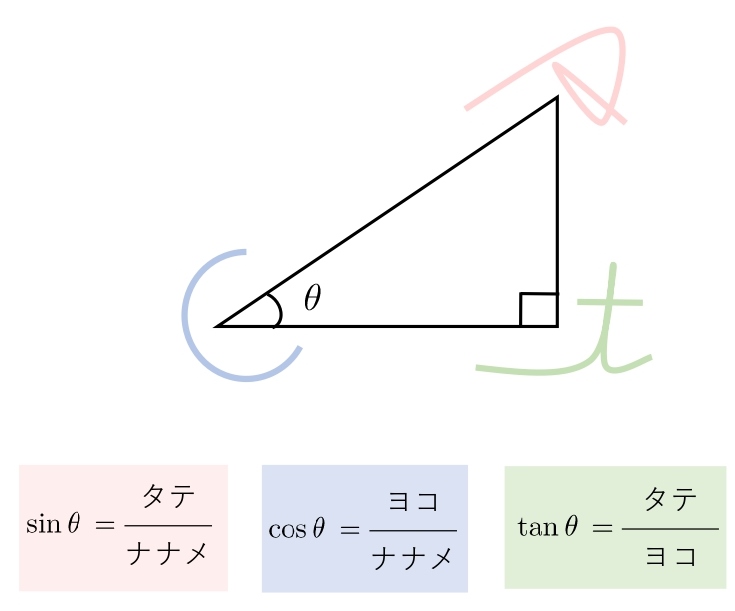
sin cos tan の 1 文字目の筆記体を「分母→分子」の順でみます。
sin の s、cos の c、tan の t を三角形の辺に沿って描くと、sin cos tan の値になります。
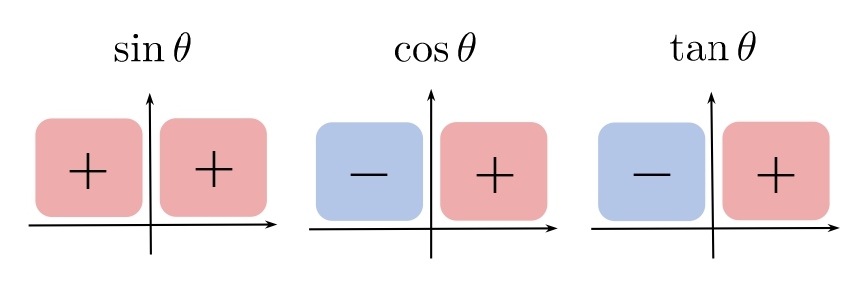
sin cos tan の符号です。
これら 3 つの公式は暗記して下さい。
この基礎知識がある前提で sin cos tan のθの求め方を説明します。
2.2 sin cos tan のθの求め方
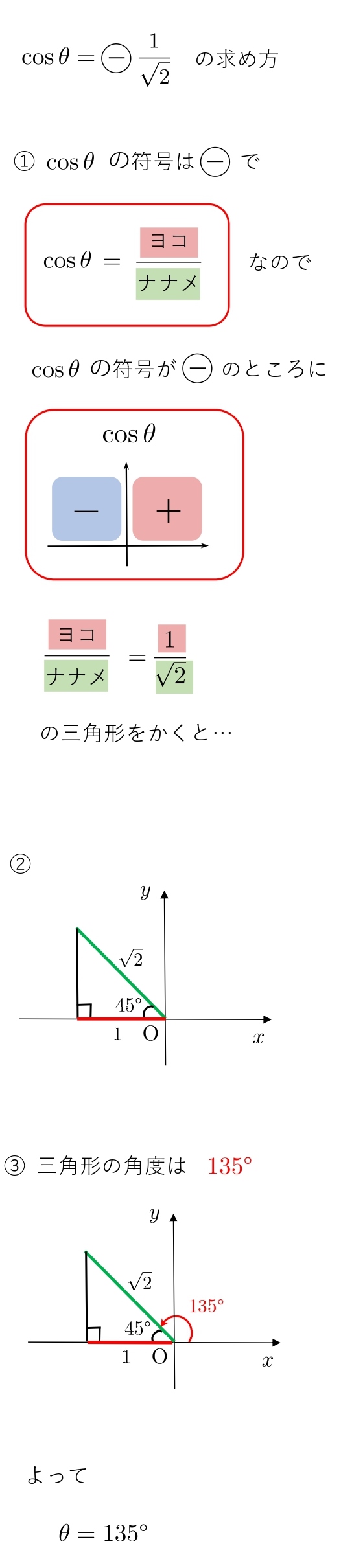
\(0≦θ≦180°\) のとき、次の方程式を解け。
(1) \( \sinθ=\displaystyle{\frac{\sqrt{3}}{2}} \)
(2) \( \cosθ=\displaystyle{-\frac{1}{\sqrt2}} \)
3. 三角比の公式一覧
数学Ⅰ「三角比」の公式一覧を、PDFファイルでA4プリント1枚にまとめました。
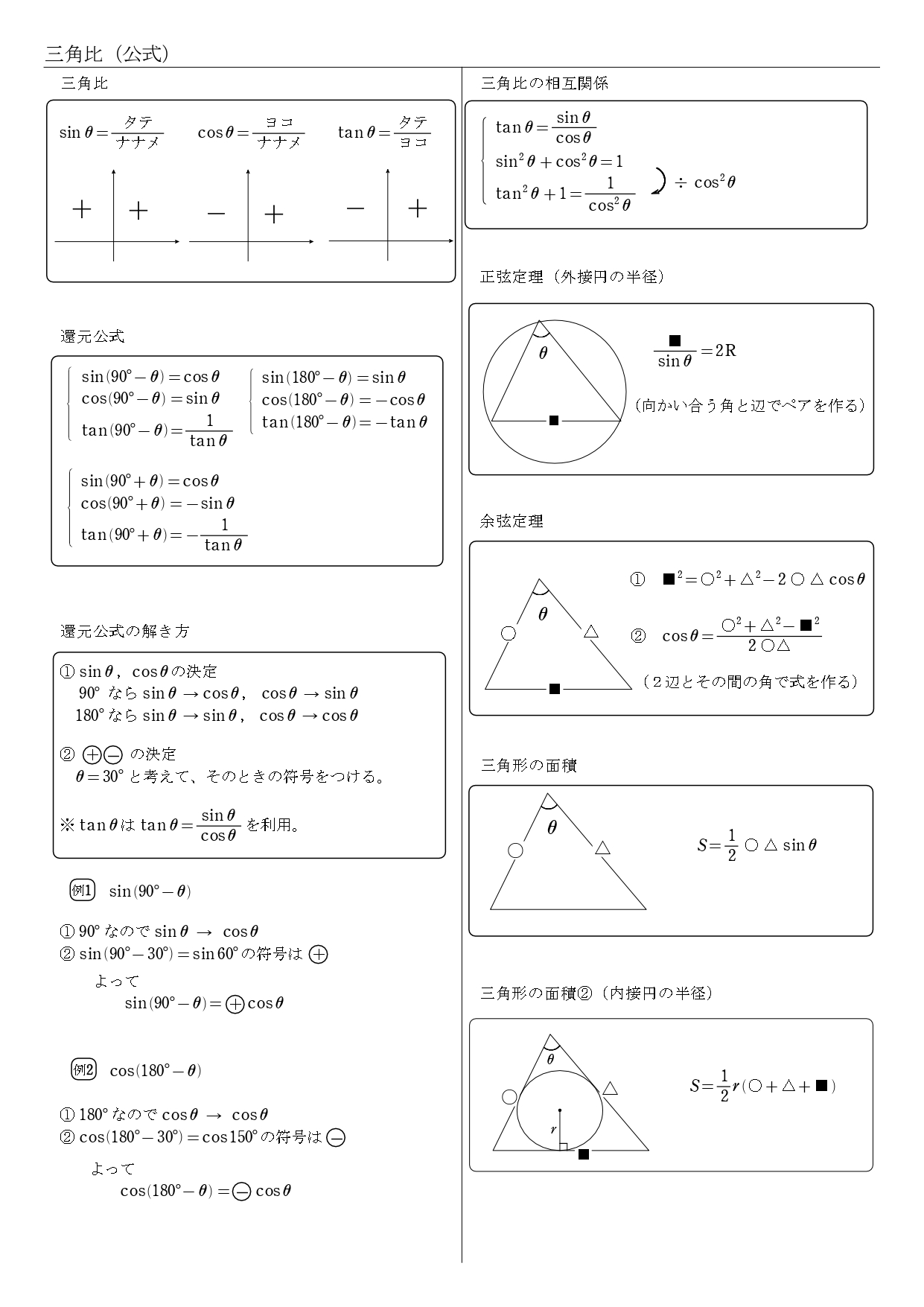
4. 三角比の問題
数学Ⅰ「三角比」の教科書の問題と解答をプリントにまとめています。
教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅するように作っています。
ぜひチェックしてみてください。
このページでは、数学Ⅰ「Þ ...

【高校数学Ⅰ】図形と計量 三角比 教科書(問題・解答・公式・解説)
